РЕШЕНИЯ

О Т В Е Т Ы

ІІ этапа (районного, городского) олимпиады

по математике

Для учащихся 8-11 классов общеобразовательных школ Витебской области

(2007-2008 учебный год)

ВИТЕБСК • 2007

РЕШЕНИЯ

Класс

№ 1. Ответ: 31,5%.

Пусть в куске было 100% полотна, после 1-го покупателя в куске осталось 100% - 25% = 75% полотна.

Второй покупатель купил 0,3 • 75% = 22,5% полотна, осталось 75% - 22,5% = 52,5% полотна.

После покупки третьим покупателем 0,4 • 52,5% = 21% полотна, осталось 52,5% - 21% = 31,5% полотна.

№ 2. Ответ: нет.

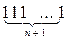2 = 1 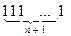+ 1 = = • (1 + 1) = а • в, а, в є N

№ 3. Треугольник с углами 60º, 30º, 90º.

		∆АВС – прямоугольный, ∆АКС – остроугольный, ∆КВС – тупоугольный, ∆АКС – равносторонний, ∆СКВ – равнобедренный, ∆АСВ – разносторонний.

№ 4. Ответ: верно.

Полагая, для определенности, а≥в, из первого равенства получим в³≥с³ , откуда в≥с. А тогда из второго равенства получим с³≥а³, откуда с≥а. Соотношения а≥в≥с≥ а означают, что а=в=с.

№ 5. 30 или 60.

Искомое число кабин обозначили через n, а длину пути, проходимого каждой кабиной за один оборот колеса, примем за 1.

Пусть колесо вращается в «положительном» направлении, т.е. так, что самое нижнее положение на нем занимают последовательно кабины с номерами 1, 2, 3 и т.д. Тогда за 20 мин. (с 10.00 до 10.20) каждый кабиной пройдено расстояние, равное k + , где k – некоторое целое неотрицательное число (число полных оборотов), а – расстояние (по окружности) от 4-й кабины до 25-й. За 60 мин. (с 10.00 до 11.00) пройдено втрое больше расстояние, т.е. 3(k + ), которое, с другой стороны, равно ℓ + 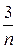, где ℓ - некоторое натуральное число, а 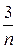– расстояние от 4-й кабины до 7-й.

Равенство 3(k + ) = ℓ + преобразуется к виду (ℓ -3k) • n = 60. Следовательно, n - делитель числа 60. А так как из условия задачи видно, что n ≥ 25, то n = 30 или n = 60.

Если же направление вращения «отрицательное», то расстояние от 4-й кабины до 25 и 7 следует брать равным 1 – и 1 – соответственно. Получим равенство.

3(k +1 – ) = ℓ + 1 – ,

где k и ℓ – некоторые целые неотрицательные числа;

отсюда (3k – 1 + 2)n = 60 и n = 30 или n = 60.

РЕШЕНИЯ

КЛАСС

№ 1. Найдем разность левой и правой частей неравенства:

а²в + в²с + с²а – в²а – а²с – с²в = ав(а – в) – с(а² – в²) + с²(а – в) =

= (а – в) (ав – ас – вс + с²) = (а – в) (в – с) (а – с).

Т.к. (а – в) (в – с) (а – с) > 0 , то а²в + в²с + с²а > в²а + а²с + с²в.

№ 2. Верно.

Полагая, для определенности, max(а; в; с) = а, из первого равенства получим в³ – с³ = в – а ≤ 0, откуда в ≤ с. Из второго равенства имеем в – с = а³ – с³ ≥ 0. Поэтому в – с = а³ – с³ = 0, откуда а = в = с.

№ 3. Ответ: р = -1, q = 0 или р = -1, q =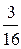

Запишем формулы Виета для данного уравнения:

Д + (1 – Д) = -р;

Д • (1 – Д) =q;

Откуда р = -1,q = Д - Д².Далее по формуле для дискриминанта имеем

Д = в²– 4q = 1 – 4q = 1 – 4 (Д – Д²), тот есть Д = 1 – 4Д + 4Д² или

4Д² – 5Д + 1 = 0

Решая последнее уравнение относительно Д, получаем

Д = 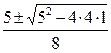= , т.е. Д = 1 иди Д = .

Если Д = 1, то q = 1 – 1² = 0. Если Д = , то q = – ( )² =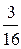

 

Поэтому либо р = -1, q = 0 или р = -1, q = .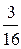

Непосредственная проверка показывает, что в этих случаях уравнение

х²+ рх + q = 0 действительно имеет корни Д и 1–Д.

 

№ 4.

		Пусть точка Т расположена внутри прямоугольника АВСД. Разобьем прямоугольник средними линиями на 4 меньших прямоугольника. Пусть, для определенности, точка Т попадает в прямоугольник МВNО. Тогда из отрезков ТА, ТС и ТД можно составить треугольник.

 

Действительно, так как точка Т лежит левее серединного перпендикуляра к отрезку АД, то ТА≤ТД. Аналогично получаем, что ТС≤ТД. Поэтому справедливы неравенства ТА + ТД > ТС и ТС + ТД > ТА. Наконец, ТА + ТС ≥ АС = ВД ≥ ТД; поэтому ТА + ТС > ТД, что и требовалось доказать.

 

№ 5. 30 или 60.

 

Ход решения такой же как и в задаче № 5 8 класса.

При «положительном» направлении вращения получается равенство 3(k +1 – ) = ℓ + 1 – , при «отрицательном» – 3(k + ) = ℓ + .