
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Класс (12-летняя школа)
№ 1. (х+2)4 + х4 = 82.
Обозначим у = х + 1,
тогда данное уравнение примет вид (у+1)4 + (у–1)4 = 82,
которое после упрощения примет вид у4 + 6у2 – 40 = 0.
Данное биквадратное уравнение имеет решение у1,2 = ±2.
Следовательно, х1 = 1, х2 = -3.
№ 2. Ответ: нет.
Допустим, что указанное nЄN существует. Тогда при некоторых k, ℓЄN выполнены неравенства 5 • 10k < 2n < 6 • 10k и 2 • 10ℓ < 5n < 3 • 10ℓ, перемножив которые, получим 10k+ℓ+1 < 10n < 18 • 10k+ℓ.
Ввиду неравенства 18 • 10k+ℓ < 10k+ℓ+2,
это означает, что k + ℓ + 1 < k + ℓ + 2, откуда (n - не натуральное). Противоречие.
№ 3.
Раскроем скобки, произвольное слагаемое в полученной сумме имеет вид: 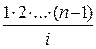 , где і = 1, 2, ..., n – 1. Сгруппируем слагаемые в этой сумме таким образом: каждое слагаемое
, где і = 1, 2, ..., n – 1. Сгруппируем слагаемые в этой сумме таким образом: каждое слагаемое 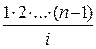 сложим со слагаемым
сложим со слагаемым  , их сумма будет равна 1•2•…•(n – 1)•(
, их сумма будет равна 1•2•…•(n – 1)•(  +
+  ) = 1•2• …•
) = 1•2• …•  .
.
Данное число будет целым, т.к. n – нечетно и і ≠ n – і. Таким образом, получаем сумму  целых чисел, каждое из которых делится на n.
целых чисел, каждое из которых делится на n.
№ 4. 30 или 60.
Ход решения такой же как и в задаче № 5 8 кл.
При «положительном» направлении вращения получается равенство  (k +1 –
(k +1 –  ) = ℓ +
) = ℓ +  , при «отрицательном» –
, при «отрицательном» –  (k +
(k +  ) = ℓ –
) = ℓ –  + 1.
+ 1.
5. Ответ:  .
.
| |||
| |||
где Р – периметр данного треугольника (отношение периметров подобных треугольников равно их коэффициенту подобия). Поэтому (  )2 + (
)2 + (  )2 = 1, откуда и получаем Р =
)2 = 1, откуда и получаем Р = 
Дата добавления: 2015-04-21; просмотров: 191; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 )2 + (
)2 + (  )2 = 1.
Но
)2 = 1.
Но 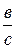 – коэффициенты подобия меньших треугольников с исходным. Их можно записать в виде
– коэффициенты подобия меньших треугольников с исходным. Их можно записать в виде  =
=  =
= 