КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Класс (11-летняя школа)
№ 1. Ответ: 1.
Так как хуz = 1, то z = 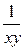 .
.
Следовательно,  +
+  +
+  =
=
= 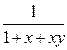 +
+  +
+ 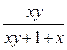 =
= 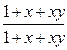 = 1
= 1
 |
№ 2.а3в - в3а > 4
а2 + в2 = 4
Рассмотрим первое неравенство:
4 < а3в - в3а , умножим обе части неравенства на 4:
16 < 4а3в - 4в3а = 2(2ав)(а2-в2) ≤ (2ав)2 + (а2-в2)2 =(а2+в2)2= 42 [второе уравнение системы] = 16, т.е. 16 < 16 – противоречие.
Значит система не имеет решения.
|
|
Из этого следует, что  АКД =
АКД =  ВЕД и значит ∆АДК = ∆ВДЕ (по первому признаку). Из равенства треугольников АДК и ВДЕ следует, что АД = ВД, значит ∆АВД – равносторонний и
ВЕД и значит ∆АДК = ∆ВДЕ (по первому признаку). Из равенства треугольников АДК и ВДЕ следует, что АД = ВД, значит ∆АВД – равносторонний и  ВАД = 60º, а
ВАД = 60º, а  АВС = 120º.
АВС = 120º.
№ 4. Ответ: 20 коров.
Обозначим всю траву на лугу за 1, прирост травы в 1 день за а. Тогда через 24 дня травы будет на лугу 1+ 24а, через 60 дней – 1+ 60а, через 96 дней 1+ 96а. Так как 70 коров съели всю траву за 24 дня, а 30 коров – за 60 дней, то количество съеденной травы 1 коровой за 1 день будет находиться как 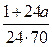 или
или 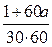 . Из уравнения
. Из уравнения 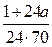 =
= 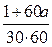 найдема, а =
найдема, а =  , тогда через 96 дней на лугу будет травы 1 + 96а = 1,2. За 1 день корова съедает
, тогда через 96 дней на лугу будет травы 1 + 96а = 1,2. За 1 день корова съедает  , а за 96 дней 0,06. Тогда 1,2 травы съедят
, а за 96 дней 0,06. Тогда 1,2 травы съедят 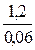 = 20 коров.
= 20 коров.
№ 5. Ответ: нет.
Пусть ρ – наибольшее из расстояний между точками, t – наименьшее.
1. Возьмем на плоскости N точек и допустим, что их можно расставить на плоскости так, что ρ – наибольшее и t – наименьшее из расстояний между ними.
2. Возьмем произвольную точку и проведем круг с центром в этой точке и радиусом ρ, тогда этот круг включает в себя все точки плоскости (т.е. они находятся внутри или на границе).
3. Около каждой точки опишем круги радиусом 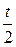 с центром в этих точках. Так как t – наименьшее, то эти круги либо не имеют общих точек (они могут только иметь общие точки в виде точек касания).
с центром в этих точках. Так как t – наименьшее, то эти круги либо не имеют общих точек (они могут только иметь общие точки в виде точек касания).
4. Суммарная площадь этих кругов 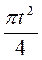 N.
N.
5. Найдем площадь круга с радиусом (ρ + 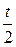 ) S = π(ρ +
) S = π(ρ + 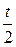 )2.
)2.
6. Очевидно 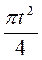 N < π(ρ +
N < π(ρ + 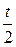 )2
)2
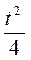 N < (ρ +
N < (ρ + 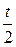 )2 ;
)2 ; 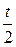
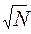 < ρ +
< ρ + 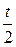
отсюда 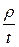 >
> 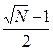 (*)
(*)
Так как ρ ≤ 21, t ≥ 3, то 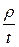 ≤ 7;
≤ 7; 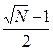 ≥ 7 – что противоречит (*).
≥ 7 – что противоречит (*).
Следовательно, нельзя.
Дата добавления: 2015-04-21; просмотров: 215; Мы поможем в написании вашей работы!; Нарушение авторских прав |