
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
класс (11-летняя школа)
№ 1.Так какх > у > z > 0, то  > 1,
> 1,  > 1 и
> 1 и  < 1
< 1
Следовательно (  – 1) (
– 1) (  – 1) (
– 1) (  – 1) < 0
– 1) < 0
 < 0
< 0
из этого (х–у)(у – z)( z –х) < 0. (*)
Рассмотрим неравенство, справедливость которого надо доказать:
 +
+  +
+  <
<  +
+  +
+ 
умножим обе части этого неравенства на хуz
х2z + у2х + z2у < х2у + у2z + z2х
(х2z – z2х) + (у2х – у2z) +( z2у – х2у) < 0
(х – z)(х – у)(z – у) < 0
(z – х)(х – у)(у – z) < 0 (**)
Из (*) и (**) следует справедливость неравенства.
№ 2. Ответ: ± 
Рассмотрим функцию
f(х) = tg10х + sin10x для 0 < х < 
f′(х) =  (1+cos12х)
(1+cos12х)
На (0;  ) f′(х)>0, следовательно функция f(х)на (0;
) f′(х)>0, следовательно функция f(х)на (0;  ) возрастает. f(
) возрастает. f(  ) =
) =  , то х =
, то х =  .
.
На (–  ;
;  ) функция f(х) является четной, следовательно х = ±
) функция f(х) является четной, следовательно х = ±  .
.
№ 3.f(19х –  ) = 0. Заметим, что если х корень данного уравнения,
) = 0. Заметим, что если х корень данного уравнения,
то у = -  – тоже корень этого уравнения, причем у ≠ х,
– тоже корень этого уравнения, причем у ≠ х,
при этом х = -  . Поэтому все корни данного уравнения можно разбить на пары. При решении данного уравнения было получено (по условию) 11 различных корней (т.е. нечетное число). Так как корни можно разбить на пары, то их количество должно быть четным. Т.е. для одного из найденных корней еще не найден парный корень. Следовательно существует еще один корень.
. Поэтому все корни данного уравнения можно разбить на пары. При решении данного уравнения было получено (по условию) 11 различных корней (т.е. нечетное число). Так как корни можно разбить на пары, то их количество должно быть четным. Т.е. для одного из найденных корней еще не найден парный корень. Следовательно существует еще один корень.
№ 4.

№ 5. Ответ: нет.
Пусть ρ – наибольшее из расстояний между точками, t – наименьшее.
7. Возьмем на плоскости N точек и допустим, что их можно расставить на плоскости так, что ρ – наибольшее и t – наименьшее из расстояний между ними.
8. Возьмем произвольную точку и проведем круг с центром в этой точке и радиусом ρ, тогда этот круг включает в себя все точки плоскости (т.е. они находятся внутри или на границе).
9. Около каждой точки опишем круги радиусом 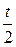 с центром в этих точках. Так как t – наименьшее, то эти круги либо не имеют общих точек (они могут только иметь общие точки в виде точек касания).
с центром в этих точках. Так как t – наименьшее, то эти круги либо не имеют общих точек (они могут только иметь общие точки в виде точек касания).
10. Суммарная площадь этих кругов 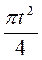 N.
N.
11. Найдем площадь круга с радиусом (ρ + 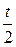 ) S = π(ρ +
) S = π(ρ + 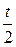 )2.
)2.
12. Очевидно 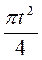 N < π(ρ +
N < π(ρ + 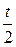 )2
)2
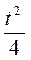 N < (ρ +
N < (ρ + 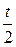 )2 ;
)2 ; 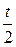
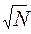 < ρ +
< ρ + 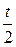
отсюда 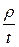 >
> 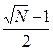 (*)
(*)
Так как ρ ≤ 21, t ≥ 3, то 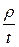 ≤ 7;
≤ 7; 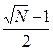 ≥ 7 – что противоречит (*).
≥ 7 – что противоречит (*).
Следовательно, нельзя.
Дата добавления: 2015-04-21; просмотров: 217; Мы поможем в написании вашей работы!; Нарушение авторских прав |