Логические и семантические парадоксы. Рациональное мышление и чувственные данные

Проблема соотношения мышления чувств.

Еще древние греки заметили трудности описания мира рациональным образом. Так Парменид указывал на сильное различие между подлинной истиной, являющейся продуктом рационального освоения действительности, и мнением, основанном на чувственном познании. Чувственные данные дают нам образ лишь кажущегося состояния вещей. С помощью чувственного познания нельзя постичь подлинную сущность вещей. Известна апория Ахиллес-черепаха, в которой Ахиллес должен пройти за конечное время бесконечное число отрезков. Все логические парадоксы имеют общее свойство, которые можно определить, как самоприменение или самоотносимость. Т.е. сущность, о которой идет речь, определяется или характеризуется посредством некоторой совокупности, которой она сама принадлежит.

Ярким примером логического научного вывода, который противоречит обыденным чувственным представлениям, является вывод о свойствах объектов в n-мерном пространстве.

Рассмотрим на плоскости квадрат со стороной 2. n=2. О(0;0), углы (±2, ±2). По углам впишем окружности радиусом 1, их центры (±1,±1). Центр окружности: . d={расстояние до ближайшей окружности}=

Теперь рассмотрим куб. n=3. .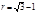

Рассмотрим n-мерное пространство, в нем рассмотрим n-мерный куб со стороной 4, по углам которого описано единичной сферы. Определим радиус сферы, который касается всех этих сфер, получаем: .

При n=10 это выражение r_n>2, т.е. вписанная по построению в n-мерный куб сфера выходит за его границы.

Маленькая сфера выходит за размеры куба. Можно показать, что при n→∞ объем n-мерного куба будет намного меньше, чем объем n-мерной сферы.

Вывод: Рассуждения, которые подтверждены данными науки, противоречат обыденным представлениям о метрических соотношениях объектов. Наши макропредставления неприемлемы к n-мерному пространству.

Теория Бреммермана

В ней рассматривается физическое ограничение на объем вычислений. Любая активная деятельность, связанная с обработкой, хранением и воспроизведением информации должна основываться на материальном носителе.

Вопрос: сколько битов информации n может храниться в теле m?

Это число из современных физических соображений:

E_max— max. количество энергии, которую мы можем извлечь из тела массой m.

E=mc²; DE—разрешение, с которым мы можем наблюдать один энергетический уровень и 1 бит кодируется одним энергетическим уровнем

DE×Dt³h—соотношение неопределенностей Гейзенберга и h-постоянная Планка, Dt—продолжительность наблюдения.

Разделив формулы друг на друга получаем формулу:

Значит, что компьютер массой в 1г за секунду не сможет обработать > чем 2×10⁴⁷бит.

Пример парадоксального расчета

Возраст Вселенной оценивается на 10¹⁷сек, ее масса оценивается 10⁵⁸г. Получаем результат: Вселенная смогла бы обработать за время свой жизни 10¹²²бит.

Возьмем аэропорт: за сутки 1000 запросов типа (да/нет). Таким аэропортом управляет 20 диспетчеров.

Вопрос: какое количество информации проходит через них?

Полное число всевозможных ответов на такие запросы определяется известной формулой количества булевых функций от 1000 переменных: .Определим количество информации:

Это число больше 10¹²²