Внутренняя энергия газа Ван-дер-Ваальса

Потенциальная энергия межмолекулярных сил взаимодействия вычисляется как работа, которую совершают эти силы, при разведении молекул на бесконечность:

Внутренняя энергия газа Ван-дер-Ваальса складывается из его кинетической энергии (энергии теплового движения молекул) и только что нами посчитанной потенциальной. Так, для одного моль газа:

где 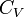— молярная теплоёмкость при постоянном объёме, которая предполагается не зависящей от температуры.

31 Пове́рхностное натяже́ние — термодинамическая характеристика поверхности раздела двух находящихся в равновесии фаз, определяемая работой обратимого изотермокинетического образования единицы площади этой поверхности раздела при условии, что температура, объём системы и химические потенциалы всех компонентов в обеих фазах остаются постоянными.

Поверхностное натяжение имеет двойной физический смысл — энергетический (термодинамический) и силовой (механический). Энергетическое (термодинамическое) определение: поверхностное натяжение — это удельная работа увеличения поверхности при её растяжении при условии постоянства температуры. Силовое (механическое) определение: поверхностное натяжение — это сила, действующая на единицу длины линии, которая ограничивает поверхность жидкости^[1].

Сила поверхностного натяжения направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует и пропорциональна длине этого участка. Коэффициент пропорциональности — сила, приходящаяся на единицу длины контура — называется коэффициентом поверхностного натяжения. Он измеряется в ньютонах на метр. Но более правильно дать определение поверхностному натяжению, как энергии (Дж) на разрыв единицы поверхности (м²). В этом случае появляется ясный физический смысл понятия поверхностного натяжения.

В 1983 году было доказано теоретически и подтверждено данными из справочников (Журнал физической химии. 1983, № 10, с. 2528—2530), что понятие поверхностного натяжения жидкости однозначно является частью понятия внутренней энергии (хотя и специфической: для симметричных молекул близких по форме к шарообразным). Приведенные в этой журнальной статье формулы позволяют для некоторых веществ теоретически рассчитывать значения поверхностного натяжения жидкости по другим физико-химическим свойствам, например, по теплоте парообразования или по внутренней энергии (подробнее о физической природе поверхностного натяжения жидкости см.соотв. статью на викиучебнике или ^[2] , ^[3])

Поверхностное натяжение может быть на границе газообразных, жидких и твёрдых тел. Обычно имеется в виду поверхностное натяжение жидких тел на границе «жидкость — газ». В случае жидкой поверхности раздела поверхностное натяжение правомерно также рассматривать как силу, действующую на единицу длины контура поверхности и стремящуюся сократить поверхность до минимума при заданных объёмах фаз.

В общем случае прибор для измерения поверхностного натяжения называется тензиометр.

Так как появление поверхности жидкости требует совершения работы, каждая среда «стремится» уменьшить площадь своей поверхности:

• в невесомости капля принимает сферическую форму (сфера имеет наименьшую площадь поверхности среди всех тел одинакового объёма).
• струя воды «слипается» в цилиндр.
• маленькие объекты с плотностью, большей плотности жидкости, способны «плавать» на поверхности жидкости, так как сила тяготения меньше силы, препятствующей увеличению площади жидкости.
• некоторые насекомые (например, водомерки) способны передвигаться по воде, удерживаясь на её поверхности за счёт сил поверхностного натяжения.
• На многих поверхностях, именуемых несмачиваемыми, вода (или другая жидкость) собирается в капли.

Сма́чивание — это поверхностное явление, заключающееся во взаимодействии жидкости с поверхностью твёрдого тела или другой жидкости. Смачивание бывает двух видов:

• Иммерсионное (вся поверхность твёрдого тела контактирует с жидкостью)
• Контактное (состоит из трёх фаз — твердая, жидкая, газообразная)

Смачивание зависит от соотношения между силами сцепления молекул жидкости с молекулами (или атомами) смачиваемого тела (адгезия) и силами взаимного сцепления молекул жидкости (когезия).

Если жидкость контактирует с твёрдым телом, то существуют две возможности:

1. молекулы жидкости притягиваются друг к другу сильнее, чем к молекулам твёрдого тела. В результате силы притяжения между молекулами жидкости собирают её в капельку. Так ведёт себя ртуть на стекле, вода на парафине или «жирной» поверхности. В этом случае говорят, что жидкость не смачивает поверхность;

2. молекулы жидкости притягиваются друг к другу слабее, чем к молекулам твёрдого тела. В результате жидкость стремится прижаться к поверхности, расплывается по ней. Так ведёт себя ртуть на цинковой пластине, вода на чистом стекле или дереве. В этом случае говорят, что жидкость смачивает поверхность.

Степень смачивания характеризуется углом смачивания. Угол смачивания (или краевой угол смачивания) это угол, образованный касательными плоскостями к межфазным поверхностям, ограничивающим смачивающую жидкость, а вершина угла лежит на линии раздела трёх фаз. Измеряется методом лежащей капли^[1]. В случае порошков надёжных методов, дающих высокую степень воспроизводимости, пока (по состоянию на 2008 год) не разработано. Предложен весовой метод определения степени смачивания, но он пока не стандартизован.

Измерение степени смачивания весьма важно во многих отраслях промышленности (лакокрасочная, фармацевтическая, косметическая и т. д.). К примеру, на лобовые стёкла автомобилей наносят особые покрытия, которые должны быть устойчивы против разных видов загрязнений. Состав и физические свойства покрытия стёкол и контактных линз можно сделать оптимальным по результатам измерения контактного угла^[2].

К примеру, популярный метод увеличения добычи нефти при помощи закачки воды в пласт исходит из того, что вода заполняет поры и выдавливает нефть. В случае мелких пор и чистой воды это далеко не так, поэтому приходится добавлять специальные ПАВ. Оценку смачиваемости горных пород при добавлении различных по составу растворов можно измерить различными приборами.

32и 33 Капиллярным давлением (p₀, Па) (англ. capillary pressure) называют разность давлений (±Δp), возникающую вследствие искривления поверхности жидкости. Такую поверхность имеют, например, капли в эмульсиях и туманах, капиллярные мениски. Обозначим давление под искривлённой поверхностью жидкости — , давление под плоской поверхностью — .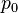

Капиллярное давление определяется уравнением

(1)

Знак капиллярного давления («плюс» или «минус») зависит от знака кривизны. Выпуклые поверхности имеют положительную кривизну. Центр кривизны выпуклой поверхности находится внутри соответствующей фазы (в данном случае — внутри жидкости). Тогда согласно уравнению (1) капиллярное давление p_c>0, то есть давление под выпуклой поверхностью жидкости больше, чем давление под плоской поверхностью: p_r>p₀. Пример дисперсной частицы с выпуклой поверхностью — капля жидкости в аэрозоле или эмульсии. Выпуклую поверхность имеет мениск несмачивающей жидкости в капилляре.

Вогнутые поверхности имеют отрицательную кривизну, поэтому капиллярное давление p_c<0 (этому случаю отвечает знак «минус» в уравнении (1)). Давление жидкости p_r под вогнутой поверхность меньше, чем под плоской: p_r<p₀. Пример вогнутой поверхности — мениск смачивающей жидкости в капилляре.

Капиллярное давление — это скачок давления (Δp) на границе двух фаз, разделённых искривлённой поверхностью.

Капиллярное давление зависит от поверхностного натяжения и кривизны поверхности. Эта связь описывает закон Лапласа (1805). Для вывода уравнения капиллярного давления найдём условие, при котором газовый пузырёк объёмом V внутри жидкости сохраняется неизменным, то есть не расширяется и не сжимается. Равновесной форме соответствует минимальное значение энергии Гиббса. При увеличении радиуса пузырька на малую величину dr изменение энергии Гиббса dG будет равно

(2)

Слагаемое p_cdV определяет работу изобарического расширения, слагаемое σdΩ — затрату работы на увеличение поверхности пузырька; Ω = 4πr² — поверхность сферического пузырька радиусом r.

При терминологическом равновесии фаз должно выполняться условие минимума энергии Гиббса: ΔG = 0; отсюда получаем

4πr²p_c + 8πrσ = 0.

В итоге находим связь между капиллярным давлением и радиусом кривизны r для вогнутой сферической поверхности:

p_c = — (2σ)/r. (3)

Отрицательный знак капиллярного давления показывает, что внутри газового пузырька давление p_r больше, чем давление p₀ в окружающей его жидкости. Именно по этой причине пузырёк не «схлопывается» под давлением окружающей его жидкости.

Аналогично выводится уравнение капиллярного давления для выпуклой поверхности жидкости, например для капли аэрозоля (тумана) в газовой фазе. Для выпуклой сферической поверхности получим

p_c = + (2σ)/r. (4)

Положительное капиллярное давление сжимает каплю. В качестве примера рассчитаем капиллярное давление для капли ртути радиусом 10 нм. Поверхностное натяжение ртути при комнатной температуре составляет σ = 473,5 мДж/м². Тогда из уравнения (4) находим, что наноразмерной капли (r = 10 нм) капиллярное давление равно 947 МПа, то есть оно на несколько порядков превышает атмосферное давление. Таким образом, для капель и пузырьков дисперсных размеров влияние капиллярного давления весьма значительно.

Уравнения (3) и (4) представляют закон капиллярного давления Лапласа для сферической поверхности. Для поверхности произвольной формы закон Лапласа имеет вид

p_c = ±σ(1/r₁ + 1/r₂), (5)

где r₁, r₂ — главные радиусы кривизны.

Для цилиндрической поверхности радиусом r₁ второй главный радиус кривизны r₂ = ∞, поэтому P_c = ±σ/r₁, то есть в 2 раза меньше, чем для сферической поверхности радиусом r.

Величина 0,5 (1/r₁ + 1/r₂) = H определяет среднюю кривизну поверхности. Таким образом, уравнение Лапласа (5) связывает капиллярное давление со средней кривизной поверхности жидкости

p_c = 2σH.

Закон Лапласа имеет определённые ограничения. Он выполняется достаточно точно, если радиус кривизны поверхности жидкости r >> b (b — молекулярный размер). Для нанообъектов это условие не выполняется, так как радиус кривизны соизмерим с молекулярными размерами.

Закон капиллярного давления имеет большое научное значение. Он устанавливает фундаментальное положение о зависимости физического свойства (давления) от геометрии, а именно от кривизны поверхности жидкости. Теория Лапласа оказала значительное влияние на развитие физикохимии капиллярных явлений, а также на некоторые другие дисциплины. Например, математическое описание искривлённых поверхностей (основы дифференциальной геометрии) было выполнено К. Гауссом именно в связи с капиллярными явлениями.

Закон Лапласа имеет много практических приложений в химической технологии, фильтрации, течении двухфазных потоков и т. д. Уравнение капиллярного давления используют во многих методах измерения поверхностного натяжения жидкостей. Закон Лапласа часто называют первым законом капиллярности.

Давление Лапласа под искривленной поверхностью жидкости.Форма поверхности жидкости, налитой в сосуд, определяется тремя факторами: силами взаимодействия между молекулами жидкости, силами взаимодействия между молекулами жидкости и молекулами, входящими в состав стенок сосуда, и действием силы тяжести.

Если достаточно большое количество жидкости налито в широкий сосуд, то жидкость вследствие преобладающего действия силы тяжести в этом случае имеет плоскую горизонтальную поверхность. Однако непосредственно у стенок сосуда поверхность жидкости несколько искривлена. Если молекулы жидкости, соприкасающиеся со стенкой сосуда, взаимодействуют с молекулами твердого тела сильнее, чем между собой, в этом случае жидкость стремится увеличить площадь соприкосновения с твердым телом. При этом поверхность жидкости изгибается вниз и говорят, что она смачивает стенки сосуда, в котором находится.

Если же молекулы жидкости взаимодействуют между собой сильнее, чем с молекулами стенок сосуда, то жидкость стремится сократить площадь соприкосновения с твердым телом, ее поверхность искривляется вверх, имеет место несмачивание жидкостью стенок сосуда.

Рис. 6.13

В узких трубочках, диаметр которых составляет доли миллиметра, искривленные края жидкости охватывают весь поверхностный слой, и вся поверхность жидкости в таких трубочках имеет вид, напоминающий полусферу. Это так называемый мениск. Он может быть вогнутым, как на рис. 6.13а, в случае смачивания, и выпуклым, как на рис. 6.13б, при несмачивании. Радиус кривизны поверхности жидкости при этом того же порядка, что и радиус трубки. Явления смачивания и несмачивания характеризуются краевым углом θ между смоченной поверхностью твердого тела и мениском в точках их соприкосновения (рис. 6.13а, б).

Наличие сил поверхностного натяжения и кривизны поверхности жидкости в капиллярной трубочке ответственно за дополнительное давление под искривленной поверхностью, называемое давлением Лапласа.

Рис. 6.14

Для вывода формулы, определяющей величину давления Лапласа, рассмотрим случай, когда поверхность жидкости в сосуде принимает форму выпуклого мениска (рис. 6.14). Пусть 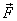– сила поверхностного натяжения, действующая по касательной к поверхности жидкости, R – радиус кривизны поверхности мениска, r – радиус кривизны сечения мениска горизонтальной плоскостью. Силу 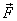можно разложить на две составляющие и . Очевидно, что при суммировании по периметру мениска все составляющие дадут ноль, и давление Лапласа будет обусловлено суммарным действием составляющих . Найдем составляющую и проведем суммирование по контуру, ограничивающему мениск в горизонтальном сечении, имея в виду, что сила поверхностного натяжения , где Δl – элемент длины контура.

,

(6.17)

.

(6.18)

Действие этой силы приходится на круговое сечение мениска площадью (рис. 6.14). Следовательно, избыточное давление Лапласа, обусловленное кривизной поверхности и действием сил поверхностного натяжения, равно

.

(6.19)

Можно обобщить полученную формулу на случай более сложной поверхности. В общем случае давление Лапласа определяется соотношением

,

(6.20)

где R₁ и R₂ – радиусы кривизны двух взаимно перпендикулярных сечений мениска.

Рис. 6.15

Радиусы кривизны, входящие в последнюю формулу, являются алгебраическими величинами. Если центр кривизны нормального сечения мениска находится под его поверхностью, то соответствующий радиус кривизны является положительной величиной (рис. 6.15а). В случае, когда центр кривизны находится над поверхностью мениска, R – отрицательно (рис. 6.15б). Отсюда следует, что под выпуклой поверхностью мениска давление Лапласа положительно (оно добавляется к атмосферному давлению Р₀), под вогнутой поверхностью мениска давление Лапласа отрицательно (оно меньше атмосферного давления Р₀ на величину Р_Л). Очевидно, что давление Лапласа тем больше, чем меньше радиус кривизны сечения, поэтому оно играет наиболее важную роль в капиллярных явлениях.

Применяя формулу Лапласа для частного случая сферической капли , находим:

.

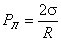(6.21)

Если поверхность мениска имеет цилиндрическую форму, то один из радиусов кривизны сечения можно считать равным бесконечности. Для этого частного случая давление Лапласа равно

.

(6.22)

В случае мыльного пузырька дополнительное давление, которое испытывает находящийся внутри него газ, равно , так как у пузырька две поверхности – наружная и внутренняя, каждая из которых создает дополнительное давление Лапласа.

Убедительной иллюстрацией существования лапласовского давления служит описанный ниже опыт.

Рис. 6.16

С помощью двух сообщающихся трубочек выдуваются мыльные пузыри (рис. 6.16), после этого трубочка С закрывается. Вследствие неизбежных случайных обстоятельств радиусы пузырей будут отличаться друг от друга. Внутри пузырька меньшего радиуса давление Лапласа больше, и воздух из него начнет перемещаться в пузырек большего радиуса. В результате большой пузырек будет увеличиваться в размерах, а маленький спустя непродолжительное время исчезнет.

34 Твёрдое тело — это одно из четырёх агрегатных состояний вещества, отличающееся от других агрегатных состояний (жидкости, газов, плазмы) стабильностью формы и характером теплового движения атомов, совершающих малые колебания около положений равновесия^[1].

Различают кристаллические и аморфные твёрдые тела. Раздел физики, изучающий твёрдые тела называется физикой твёрдого тела.

Технические приспособления, созданные человеком, используют различные свойства твёрдого тела. В прошлом твёрдое тело применялось как конструкционный материал и в основе употребления лежали непосредственно ощутимые механические свойства как то твёрдость, масса, пластичность, упругость, хрупкость. В современном мире применение твёрдого тела основывается на физических свойствах, которые зачастую обнаруживаются только при лабораторных исследованиях.