Характеристики.

• Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы, (м)
• Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), (с)
• Частота — число колебаний в единицу времени, (Гц, с⁻¹).

Период колебаний и частота — обратные величины;

и

В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота 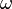(рад/с, Гц, с⁻¹), показывающая число колебаний за 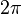единиц времени:

• Смещение — отклонение тела от положения равновесия. Обозначение Х, Единица измерения — метр.
• Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.

36 Гармони́ческий осцилля́тор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука):

где k — коэффициент жёсткости системы.

Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор (см. LC-цепь).

Ма́ятник — система, подвешенная в поле тяжести и совершающая механические колебания. Колебания совершаются под действием силы тяжести, силы упругости и силы трения. Во многих случаях трением можно пренебречь, а от сил упругости (либо сил тяжести) абстрагироваться, заменив их связями.

Во время колебаний маятника происходят постоянные превращения энергии из одного вида в другой. Кинетическая энергия маятника превращается в потенциальную энергию (гравитационную, упругую) и обратно. Кроме того, постепенно происходит диссипация кинетической энергии в тепловую за счёт сил трения.

Одним из простейших маятников является шарик, подвешенный на нити. Идеализацией этого случая является математический маятник — механическая система, состоящая из материальной точки, подвешенной на невесомой нерастяжимой нити или на невесомом стержне в поле тяжести.

Если размерами массивного тела пренебречь нельзя, но всё еще можно не учитывать упругих колебаний тела, то можно прийти к понятию физического маятника. Физический маятник — твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной горизонтальной оси, не проходящей через центр масс этого тела.

Система из нескольких шариков, подвешенных на нитях в одной плоскости, колеблющихся в этой плоскости и соударяющихся друг с другом, называется маятником Ньютона. Здесь уже приходится учитывать упругие процессы.

Маятник Фуко — это груз, подвешенный на нити, способный изменять плоскость своих колебаний.

Ещё одним простейшим маятником является пружинный маятник. Пружинный маятник — это груз, подвешенный на пружине и способный колебаться вдоль вертикальной оси.

Крутильный маятник — механическая система, представляющая собой тело, подвешенное в поле тяжести на тонкой нити и обладающее лишь одной степенью свободы: вращением вокруг оси, задаваемой неподвижной нитью.

Маятники используются в различных приборах, например, в часах и сейсмографах.

Маятники облегчают изучение колебаний, так как наглядно демонстрируют их свойства.

40 Волна́ — изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами, «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины — например, плотности вещества, напряжённости электрического поля, температуры^[1]».

В связи с этим волновой процесс может иметь самую разную физическую природу: механическую, химическую (реакция Белоусова — Жаботинского, протекающая в автоколебательном режиме каталитического окисления различных восстановителей бромисто-водородной кислотой HBrO₃ ), электромагнитную (электромагнитное излучение), гравитационную (гравитационные волны), спиновую (магнон), плотности вероятности (ток вероятности) и т. д.

Многообразие волновых процессов приводит к тому, что никаких абсолютных общих свойств волн выделить не удаётся^[2]. Одним из часто встречающихся признаков волн считается близкодействие, проявляющееся во взаимосвязи возмущений в соседних точках среды или поля, однако в общем случае может отсутствовать и оно^[2].

Среди всего многообразия волн выделяют некоторые их простейшие типы, которые возникают во многих физических ситуациях из-за математического сходства описывающих их физических законов^[2]. Об этих законах говорят в таком случае как о волновых уравнениях. Для непрерывных систем это обычно дифференциальные уравнения в частных производных в фазовом пространстве системы, для сред часто сводимые к уравнениям, связывающим возмущения в соседних точках через пространственные и временные производные этих возмущений^[2]. Важным частным случаем волн являются линейные волны, для которых справедлив принцип суперпозиции.

По своему характеру волны подразделяются на^{[источник не указан 470 дней]}:

• По признаку распространения в пространстве: стоячие, бегущие.
• По характеру волны: колебательные, уединённые (солитоны).
• По типу волн: поперечные, продольные, смешанного типа.
• По законам, описывающим волновой процесс: линейные, нелинейные.
• По свойствам субстанции: волны в дискретных структурах, волны в непрерывных субстанциях.
• По геометрии: сферические (пространственные), одномерные (плоские), спиральные.

Отличие колебания от волны.

Бегущие волны, как правило, способны удаляться на значительные расстояния от места своего возникновения (по этой причине волны иногда называют «колебанием, оторвавшимся от излучателя»^{[источник не указан 470 дней]}).

В основном физические волны не переносят материю, но возможен вариант, где происходит волновой перенос именно материи, а не только энергии. Такие волны способны распространяться сквозь абсолютную пустоту. Примером таких волн может служить нестационарное излучение газа в вакуум, волны вероятности электрона и других частиц, волны горения, волны химической реакции, волны плотности реагентов, волны плотности транспортных потоков. Бегущая волна — волновое движение, при котором поверхность равных фаз (фазовые волновые фронты) перемещается с конечной скоростью (постоянной для однородной среды). С бегущей волной, групповая скорость которой отлична от нуля, связан перенос энергии, импульса или других характеристик процесса^[1]. Бегущая волна - волна, которая при распространении в среде переносит энергию (в отличие от стоячей волны). Примеры: упругая волна в стержне, столбе газа, жидкости, электромагнитная волна вдоль длинной линии, в волноводе^[2]. Бегущая волна — волновое возмущение, изменяющееся во времени и пространстве согласно выражению

где — амплитудная огибающая волны, — волновое число и — фаза колебаний. Фазовая скорость этой волны даётся выражением

где — это длина волны.

При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:

• результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.

Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.

Принцип суперпозиции может принимать и иные формулировки, которые полностью эквивалентны приведённой выше:

• Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя.
• Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.
• Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.

Именно линейность фундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции.