Частные случаи

В одномерных средах без дисперсии групповая скорость формально совпадает с фазовой скоростью лишь в случае одномерных волн. В диссипативных (поглощающих) средах групповая скорость уменьшается с увеличением частоты в случае нормальной дисперсии фазовой скорости и, наоборот, увеличивается в средах с аномальной дисперсией. Если дисперсионные свойства среды таковы, что волновой пакет распространяется в ней без существенных изменений формы своей огибающей, групповая скорость обычно может быть интерпретирована как скорость переноса «энергии» волны и скорость, с которой могут быть переданы с помощью волнового пакета сигналы, несущие информацию, (то есть «скорость распространения причинности»).

В классическом пределе квантовомеханических уравнений скорость классической частицы представляет собой значение групповой скорости соответствующей квантовомеханической волновой функции. Одно из пары канонических уравнений Гамильтона:

— есть, таким образом, классический предел приведенного выше выражения для групповой скорости; это особенно ясно в декартовых координатах, учитывая

Основными свойствами волн являются:

1) поглощение;2) рассеяние;3) отражение;4) преломление;5) интерференция;6) дифракция7) дисперсия;8) поляризация.

Следует заметить, что волновую природу любого процесса доказывают явления интерференции и дифракции.

Рассмотрим некоторые свойства волн более подробно:

1.Образование стоячих волн

При наложении прямой и отраженной бегущих волн возникает стоячая волна. Она называется стоячей, так как, во-первых, узлы и пучности в пространстве не перемещаются, во-вторых, она не переносит энергию в пространстве.

Стоячая волна образуется устойчивая, если на длине L укладывается целое число полуволн.

Любое упругое тело (например, струна) при свободных колебаниях имеет основной тон и обертоны. Чем больше обертонов имеет упругое тело, тем красивее оно звучит.

Примеры применения стоячих волн:

- духовые музыкальные инструменты (орган, труба)- струнные музыкальные инструменты (гитара, пианино, скрипка)- камертоны

2.Интерференция волн

Интерференция волн - устойчивое распределение с течением времени амплитуды колебаний в пространстве при наложении когерентных волн.

Примечание. Волны можно считать когерентными, если:

- они имеют одинаковые частоты;- сдвиг по фазе волн, пришедших в данную точку, величина постоянная, то есть не зависит от времени.

В данной точке при интерференции наблюдается минимум, если разность хода волн равна нечетному числу полуволн.

В данной точке при интерференции наблюдается максимум, если разность хода волн равна четному количеству полуволн или целому числу длин волн.

При интерференции происходит перераспределение энергии волн, то есть в точку минимума она почти не поступает, а в точку максимума её поступает больше.

3.Дифракция волн.

Волны способны огибать препятствия. Так, морские волны свободно огибают выступающий из воды камень, если его размеры меньше длины волны или сравнимы с ней. За камнем волны распространяются так, как если бы его не было совсем. Точно так же волна от брошенного в пруд камня огибает торчащий из воды прутик. Только за препятствием большого, по сравнению с длиной волны, размера образуется "тень": волны за препятствие не проникают.

Способностью огибать препятствия обладают и звуковые волны. Вы можете слышать сигнал машины за углом дома, когда самой машины не видно. В лесу деревья заслоняют ваших товарищей. Чтобы их не потерять, вы начинаете кричать. Звуковые волны, в отличие от света, свободно огибают стволы деревьев и доносят ваш голос до товарищей.

итак, ДИФРАКЦИЯ - явление нарушения закона прямолинейного распространения волн в однородной среде или огибание препятствий волнами.

На пути волны экран с щелью:

	Длина щели много больше длины волны. Дифракция не наблюдается.
	Длина щели соизмерима с длиной волны. Дифракция наблюдается.

На пути волны преграда:

	Размер преграды много больше длины волны. Дифракция не наблюдается.
	Размер преграды соизмерим с длиной волны. Дифракция наблюдается (волна огибает препятствие).

УСЛОВИЕ НАБЛЮДЕНИЯ ХОРОШЕЙ ДИФРАКЦИИ: длина волны соизмерима с размерами препятствия, щели или преграды.

43 Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.

Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе^[1]; в природе — волны Шумана.

Чисто стоячая волна, строго говоря, может существовать только при отсутствии потерь в среде^[2] и полном отражении волн от границы. Обычно, кроме стоячих волн, в среде присутствуют и бегущие волны, подводящие энергию к местам её поглощения или излучения.

Для демонстрации стоячих волн в газе используют трубу Рубенса.

В случае гармонических колебаний в одномерной среде стоячая волна описывается формулой:

,

где u — возмущения в точке х в момент времени t, — амплитуда стоячей волны, 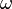— частота , k — волновой вектор, — фаза.

Стоячие волны являются решениями волновых уравнений. Их можно представить себе как суперпозицию волн, распространяющихся в противоположных направлениях.

При существовании в среде стоячей волны, существуют точки, амплитуда колебаний в которых равна нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания имеют максимальную амплитуду, называются пучностями.

Моды .Стоячие волны возникают в резонаторах. Конечные размеры резонатора накладывают дополнительные условия на существование таких волн. В частности, для систем конечных размеров волновой вектор (а, следовательно, длина волны) может принимать лишь определенные дискретные значения. Колебания с определенными значениями волнового вектора называются модами. Например, различные моды колебаний зажатой на концах струны определяют её основной тон и обертоны.