Примеры нарушения электродинамического принципа суперпозиции

Если рассматривается электродинамика не в вакууме, а в какой-либо среде, то принцип суперпозиции может нарушаться. Так, например, если поляризуемость или намагниченность среды нелинейно зависят от приложенного поля, это приводит к нелинейным поправкам в уравнениях Максвелла. Прямым следствием этого является нарушение принципа суперпозиции в такой нелинейной среде.

В некоторых случаях эти нелинейности невелики, и принцип суперпозиции с некоторой степенью приближения может выполняться. В других случаях нарушение принципа суперпозиции велико и может приводить к принципиально новым явлениям. Так, например, два луча света, распространяющиеся в нелинейной среде, могут изменять траекторию друг друга. Более того, даже один луч света в нелинейной среде может воздействовать сам на себя и изменять свои характеристики. Многочисленные эффекты такого типа изучает нелинейная оптика. Принцип суперпозиции нарушается также в вакууме при учёте квантовых явлений. В квантовой электродинамике фотон может на некоторое время превратиться в электрон-позитронную пару, которая уже может взаимодействовать с другими фотонами. Эффективно это приводит к тому, что фотоны могут взаимодействовать друг с другом. Такого типа процессы (рассеяние света на свете и другие процессы нелинейной электродинамики) наблюдались экспериментально.

Групповая скорость — это величина, характеризующая скорость распространения «группы волн» - то есть более или менее хорошо локализованной квазимонохроматической волны (волны с достаточно узким спектром). Обычно интерпретируется как скорость перемещения максимума амплитудной огибающей квазимонохроматического волнового пакета (или цуга волн). В случае рассмотрения распространения волн в пространстве размерностью больше единицы подразумевается как правило волновой пакет близкий по форме к плоской волне.

Групповая скорость во многих важных случаях определяет скорость переноса энергии и информации квазисинусоидальной волной (хотя это утверждение в общем случае требует серьёзных уточнений и оговорок). Групповая скорость определяется динамикой физической системы, в которой распространяется волна (конкретной среды, конкретного поля итп). В большинстве случаев подразумевается линейность этой системы (точно или приближенно).

Для одномерных волн групповая скорость вычисляется из закона дисперсии:

,

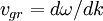где 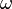— угловая частота, 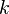— волновое число.

Групповая скорость волн в пространстве (например, трехмерном или двумерном) определяется градиентом частоты по волновому вектору :

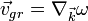
или (для трехмерного пространства):

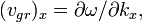
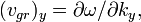
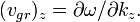
• Замечание: групповая скорость вообще говоря зависит от волнового вектора (в одномерном случае - от волнового числа), то есть вообще говоря различна для разной величины и для разных направлений волнового вектора.