Математическое описание стоячих волн

В одномерном случае две волны одинаковой частоты, длины волны и амплитуды, распространяющиеся в противоположных направлениях (например, навстречу друг другу), будут взаимодействовать, в результате чего может возникнуть стоячая волна. Например, гармоничная волна, распространяясь вправо, достигая конца струны, производит стоячую волну. Волна, что отражается от конца, должна иметь такую ​​же амплитуду и частоту, как и падающая волна.

Рассмотрим падающую и отраженную волны в виде:

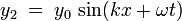
где:

• y₀ — амплитуда волны, 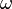— циклическая (угловая) частота, измеряемая в радианах в секунду, k — волновой вектор, измеряется в радианах на метр, и рассчитывается как 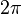поделённое на длину волны 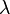, x и t — переменные для обозначения длины и времени.

Поэтому результирующее уравнение для стоячей волны y будет в виде суммы y₁ и y₂:

Используя тригонометрические соотношения, это уравнение можно переписать в виде:

Если рассматривать моды 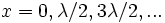и антимоды , то расстояние между соседними модами / антимодами будет равно половине длины волны .