Суть универсального теста Маурера.

При тестировании некоторой двоичной последовательности x = x₀, x₁,…,x_n-1 вычисляется статистика X_U. Сначала необходимо выбрать параметр LÎ[6,16]. Тестируемая последовательность разбивается на непересекающиеся блоки по L бит. В случае, если длина последовательности n не кратно числу L, лишние старшие биты последовательности отбрасываются. Общее количество блоков, необходимых для тестирования определяется как:

N_бл = Q + K,

где Q ³ 10·2^L;

K ³ 1000·2^L.

Значение Q выбирается таким для того, чтобы обеспечить достаточную вероятность того, что любой блок как минимум один раз встретится среди всех возможных L-битных блоков.

Таким образом, параметры Q,K и L задают необходимую длину последовательности, которая составит n ³ 1010·2^L·L, бит.

Для проверки последовательности используется двусторонний критерий с уровнем значимости 0,001 < a < 0,01. На основе полученного значения Х_u вычисляется параметр Z_u = (X_u-m)/s.

Распределение случайной величины Z_u подчиняется стандартному нормальному закону распределения с математическим ожиданием равным 0 и дисперсией равной 1.

40. Фізичний датчик Гряда 1М.

41. Основні вимоги до криптостійкого генератора псевдо випадкових послідовностей (ПВП).

К криптографически стойкому ГПСП предъявляются 3 основных требования:

1) Период ПСП (гаммы) должен быть достаточно большим для шифрования сообщений различной длины, т.к. по завершению периода числа будут повторяться, и их можно будет предсказать. Таким образом, чем длиннее ключ, тем сложнее его подобрать. Длина периода ПСП (гаммы) зависит от выбранного алгоритма получения ПСЧ;

2) ПСП должна быть практически непредсказуемой, что означает невозможность предсказать следующий бит гаммы, даже зная тип генератора и предшествующий кусок ПСП (гаммы). Чтобы гамма считалась непредсказуемой (истинно случайной), необходимо, чтобы ее период был очень большим, а различные комбинации битов определенной длины были равномерно распределены по всей ее длине;

3) Генерирование ПСП (гаммы) не должно вызывать больших технических сложностей, что обуславливает возможность практической реализации генератора программным или аппаратным путем с обеспечением необходимого быстродействия.

42. Критерій Мізеса (w²⁾

В качестве меры различия теоретической функции распределения F(x) и эмпирической F_n(x) по

критерию Мизеса (w ²) выступает средний квадрат отклонений по всем значениям аргумента x:

.

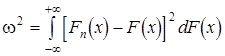На практике выражение для расчета w² заменяют выражением

,

где x_k – k-й элемент вариационного ряда; F(x_k) – значение гипотетической функции распределения в точке x_k.

При неограниченном увеличении n существует предельное распределение статистики nw _n². Задав значение вероятности a можно определить критические значения nw _n²(a ). Проверка гипотезы о законе распределения осуществляется обычным образом: если фактическое значение nw _n²окажется больше критического или равно ему, то согласно критерию Мизеса с уровнем значимости a гипотеза Н_о о том, что закон распределения генеральной совокупности соответствует F(x), должна быть отвергнута.

43. Критерій Колмогорова.

Он основан на распределении величины D_n = max |F_n(x) – F(x)|,

где F_n(x) – эмпирический закон распределения; F(x) – гипотетический закон распределения.

Критерий Колмогорова позволяет проверить согласованность распределений по малым выборкам и его часто применяют на практике. Но требуется учитывать два обстоятельства.

Во-первых, в точном соответствии с условиями его применения необходимо пользоваться следующим соотношением

Во-вторых, условия применения критерия предусматривают, что теоретическая функция распределения известна полностью (известны вид функции и ее параметры).

Статистика D_n имеет определенное распределение (распре­де­ле­ние Колмогорова) протабулированное для некоторых значений n. При n ³ 10 для определения порогового значения D_n(a) на отрезке 0,01 £ a £ 0,2 следует пользоваться формулой:

При n ³ 100 указанная формула верна для всех 0,0001 £ a £ 0,5.

Если в результате опыта окажется, что D_n ³ D_n(a) то гипотезу о согласии эмпирического и гипотетического законов распределения следует отвергнуть с уровнем значимости a.

44. Фізичні датчики випадкових процесів. Схема.