
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доказательство.
Сначала докажем первое утверждение.
Пусть система векторов 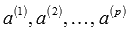 линейно зависима, тогда существует хотя бы одно отличное от нуля число
линейно зависима, тогда существует хотя бы одно отличное от нуля число  и при этом верно равенство
и при этом верно равенство 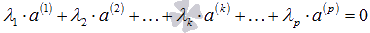 . Это равенство можно разрешить относительно
. Это равенство можно разрешить относительно 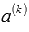 , так как
, так как 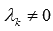 , при этом имеем
, при этом имеем

Следовательно, вектор 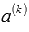 линейно выражается через остальные векторы системы
линейно выражается через остальные векторы системы 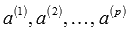 , что и требовалось доказать.
, что и требовалось доказать.
Теперь докажем второе утверждение.
Так как система векторов 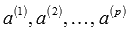 линейно независима, то равенство
линейно независима, то равенство 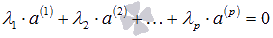 возможно лишь при
возможно лишь при 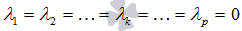 .
.
Предположим, что какой-нибудь вектор системы 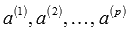 выражается линейно через остальные. Пусть этим вектором является
выражается линейно через остальные. Пусть этим вектором является 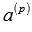 , тогда
, тогда  . Это равенство можно переписать как
. Это равенство можно переписать как 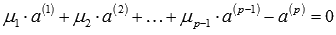 , в его левой части находится линейная комбинация векторов системы, причем коэффициент перед вектором
, в его левой части находится линейная комбинация векторов системы, причем коэффициент перед вектором 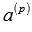 отличен от нуля, что указывает на линейную зависимость исходной системы векторов. Так мы пришли к противоречию, значит, свойство доказано.
отличен от нуля, что указывает на линейную зависимость исходной системы векторов. Так мы пришли к противоречию, значит, свойство доказано.
Из двух последних свойств следует важное утверждение:
если система векторов содержит векторы 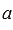 и
и 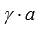 , где
, где 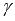 – произвольное число, то она линейно зависима.
– произвольное число, то она линейно зависима.
18.Линейная зависимость и независимость системы векторов. Доказательство теорем о линейной зависимости.
Векторы  называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 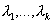 , не все равные нулю, что
, не все равные нулю, что  . Ясно, что заданные векторы будут линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные.
. Ясно, что заданные векторы будут линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные.
В противном случае, т.е. когда соотношение  выполняется только при
выполняется только при 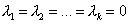 , эти векторы называютсялинейно независимыми.
, эти векторы называютсялинейно независимыми.
Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство:
- Действительно, пусть имеем два коллинеарных вектора
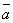 и
и 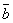 . Тогда либо оба они равны нулю, и следовательно, любая их линейная комбинация
. Тогда либо оба они равны нулю, и следовательно, любая их линейная комбинация 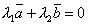 при любых λ1 и λ2, либо один из них не нуль, тогда другой отличается от него на числовой множитель, например,
при любых λ1 и λ2, либо один из них не нуль, тогда другой отличается от него на числовой множитель, например, 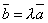 . Но отсюда
. Но отсюда 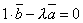 , а это и означает линейную зависимость векторов
, а это и означает линейную зависимость векторов 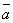 и
и 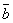 .
. - Докажем обратное, т.е. если два вектора линейно зависимы, то они коллинеарны. Пусть векторы
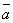 и
и 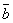 линейно зависимы. Тогда найдутся числа λ1 и λ2 такие, что
линейно зависимы. Тогда найдутся числа λ1 и λ2 такие, что 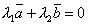 , причём, например, λ2 ≠ 0. Тогда
, причём, например, λ2 ≠ 0. Тогда  , т.е. векторы коллинеарны.
, т.е. векторы коллинеарны.
Таким образом, теорема утверждает, что линейно независимыми на плоскости могут быть только те векторы, которые неколлинеарны.
19.Диагональная система векторов. Доказательство теоремы о диагональной системе векторов.
Диагональная система векторов, система единичных векторов.
20.Система единичных векторов. Доказательство утверждений о системе единичных векторов.
Единичный вектор - это вектор, абсолютная величина (модуль) которого равен единице.
21.Базис, ранг системы векторов и векторного пространства. Доказательство теоремы о разложении вектора по базису.
22.Евклидово пространство. Определение и примеры. Норма и ее свойства. Доказательство неравенства Коши – Буняковского.
23.Ортогональные системы векторов в евклидовом пространстве. Доказательство теоремы о базисе евклидова пространства.
24.Ортогональный и ортонормированный базис. Вывод формулы для координат вектора в ортонормированном базисе.
Так как евклидово пространство является линейным, на него переносятся все понятия и свойства, относящиеся к линейному пространству, в частности, понятия базиса и размерности.
Базис 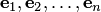 евклидова пространства называется ортогональным, если все образующие его векторы попарно ортогональны, т.е.
евклидова пространства называется ортогональным, если все образующие его векторы попарно ортогональны, т.е.
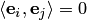 при
при 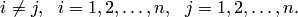
Базис 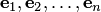 евклидова пространства называется ортонормированным, если его векторы попарно ортогональны и длина каждого из них равна единице:
евклидова пространства называется ортонормированным, если его векторы попарно ортогональны и длина каждого из них равна единице:
Теорема 8.5. В конечномерном евклидовом пространстве любую систему ортогональных (ортонормированных) векторов можно дополнить до ортогонального (ортонормированного) базиса.
25.Доказательство теоремы о необходимом и достаточном условии равенства нулю определителя.
26.Ранг матрицы. Различные формы определения ранга. Доказательство теоремы о базисном миноре. Свойства ранга. Методы нахождения.
27.Общая теория систем ЛАУ. Доказательство критерий Кронекера-Капелли.
28.Однородная система ЛАУ. Доказательство теоремы о необходимом и достаточном условии существования ненулевого решения однородной системы. Следствия.
29.Свойства решений однородной системы ЛАУ. Фундаментальная система решений однородной системы и ее нахождение.
30.Собственные векторы и собственные значения, доказательство свойства. Характеристический многочлен. Спектр.
Пусть 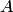 — числовая квадратная матрица n-го порядка. Ненулевой столбец
— числовая квадратная матрица n-го порядка. Ненулевой столбец 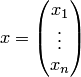 , удовлетворяющий условию
, удовлетворяющий условию
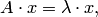
| (7.13) |
называется собственным вектором матрицы 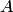 . Число
. Число 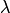 в равенстве (7.13) называется собственным значением матрицы
в равенстве (7.13) называется собственным значением матрицы 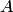 . Говорят, что собственный вектор
. Говорят, что собственный вектор 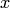 соответствует {принадлежит) собственному значению
соответствует {принадлежит) собственному значению 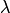 .
.
31.Теорема о сумме и произведении собственных значений. Проблема диагонализации. Теорема о построении диагональной формы матрицы.
32.Линейные преобразования переменных. Матрица линейного преобразования. Ортогональное линейное преобразование переменных.
Дата добавления: 2015-04-18; просмотров: 733; Мы поможем в написании вашей работы!; Нарушение авторских прав |