Линейное преобразование переменных.

Линейным преобразованием переменных называется такой переход от системы n переменных к системе n переменных , при котором старые переменные выражаются через новые при помощи линейных формул

или, подробнее,

(

33.Ортогональная матрица. Доказательство теоремы о необходимом и достаточном условии ортогональности матрицы. Следствия.

Ортогональная матрица порядка n матрица

Следствие 1. Модуль определителя ортогональной матрицы равен единице.

Следствие 2. Ортогональная матрица является невырожденной матрицей.

Следствие 3. Произведение двух ортогональных матриц есть ортогональная матрица.

Следствие 4. РавенствоВыражает необходимое и доста

Точное условие ортогональности матрицы

Следствие 5. Матрица, полученная транспонированием ортогональной матрицы, является ортогональной.

Следствие 6. Матрица, обратная ортогональной матрице, является ортогонал ьной.

произведение которой на транспонированную матрицу А' даёт единичную матрицу, то есть АА' = Е (а следовательно, и A'A = Е).

34.Симметрическая матрица. Теорема о собственных векторах симметрической матрицы. Проблема диагонализации симметрических матриц.

Симметричной называют квадратную матрицу, элементы которой симметричны относительно главной диагонали.

35.Квадратичная форма и ее матрица. Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования.

Канонический вид квадратичной формы
Квадратичная форма называется канонической, если все т. е.

Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.

1. Ортогональное преобразование пространства :

где - собственные значения матрицы A.

36.Положительно определенные и отрицательно определенные квадратичные формы. Связь знакоопределенности квадратичной формы с собственными значениями матрицы. Критерий Сильвестра.

Квадратичная форма A(x,x) называется положительно (отрицательно) определённой, если для любого x≠ 0 A(x,x) > 0 (A(x,x) < 0). Положительно определённые и отрицательно определённые формы называются знакоопределёнными.

Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.

Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.

37.Применение квадратичных форм для исследования кривых второго порядка.

В общем случае кривая второго порядка в базисе 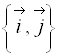описывается

уравнением 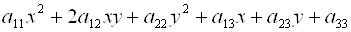. Ее первые три слагаемые образуют квадратичную форму 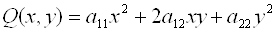с матрицей:

.

Задача о приведении кривой 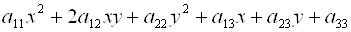к каноническому виду сводится к задаче о приведении к каноническому виду квадратичной формы 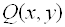этой кривой.

Пусть и 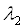– собственные значения матрицы 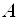, а и – ортонормированные собственные векторы матрицы 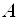, соответствующие собственным значениям и .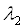

Ортонормированные векторы и называются главными направлениями этой кривой.

Пусть 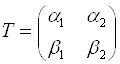является матрицей перехода от ортонормированного базиса 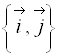к ортонормированному базису .

Тогда ортогональное преобразование:

Приводит квадратичную форму 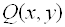к каноническому виду 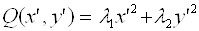, а уравнение кривой – к виду 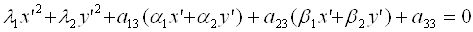в прямоугольной декартовой системе координат , оси которой направлены вдоль векторов , а начало совпадает с точкой системы координат .

Выделив в этом уравнении полные квадраты, получим 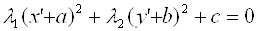, где – некоторые числа. Осуществив параллельный перенос системы координат в новое начало , получим канонический вид уравнения в системе координат . В зависимости от чисел эта кривая будет эллипсом, гиперболой, параболой, парой прямых, точкой или мнимой кривой.

38.Системы координат на плоскости (декартова и полярная). Основные приложения метода координат на плоскости с выводами формул.

Декартова система координат на плоскости определяется некоторой ее точкой O и базисом из двух векторов, параллельных плоскости. Точка O называется началом координат. Прямые, проведенные через начало координат в направлении базисных векторов, называются осями координат. Они лежат в плоскости и называются осями абсцисс и ординат. Каждая ось координат является числовой осью с началом в точке O, положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора.

Координатами точки M называются координаты вектора OM (радиус–вектора) (см. рис. 1).

Если базис ортонормированный, то связанная с ним декартова система координат называется прямоугольной.

На плоскости часто употребляется также полярная система координат (рис. 2).

Она определяется точкой O, называемой полюсом, и лучом, исходящим из полюса, называемым полярной осью. Полярными координатами ρ и j точки M называются расстояние ρ от полюса до точки M ( ρ = |OM|) и угол j между полярной осью и вектором OM (рис. 2). Угол j называется полярным углом, измеряется в радианах и отсчитывается от полярной оси против часовой стрелки. Полярные координаты точки O: ρ = 0, угол j не определен. У остальных точек ρ > 0 и угол j определен с точностью до 2π. Обычно полагают 0 ≤ j < 2 π или − π < j ≤ π.

Если полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось — с положительной частью оси абсцисс, то декартовы координаты x и y точки M выражаются через ее полярные координаты ρ и j формулами

x = ρcosj y = ρsinj .

Полярные координаты ρ и j точки M выражаются через ее декартовы координаты x и y формулами

Замечание. Если не указано положение полюса и полярной оси относительно декартовой системы координат, то считаем, что полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось — с положительной частью оси абсцисс.

39.Прямая на плоскости. Различные виды уравнения прямой. Теорема об общем уравнении прямой. Угол между двумя прямыми на плоскости. Условие параллельности и перпендикулярности двух прямых на плоскости.

40.Эллипс. Доказательство теоремы о необходимом и достаточном условии того, что точка M(x;y) лежит на эллипсе. Параметры эллипса, исследование формы по уравнению.

41.Гипербола. Доказательство теоремы о необходимом и достаточном условии того, что точка M(x;y) лежит на гиперболе. Параметры гиперболы, исследование формы по уравнению, различные возможности расположения гиперболы относительно координатных осей.

42.Парабола. Доказательство теоремы о необходимом и достаточном условии того, что точка M(x;y) лежит на параболе. Различные возможности расположения параболы относительно координатных осей. Фокальное свойство выпуклого параболического зеркала.

43.Плоскость в пространстве. Различные виды уравнения плоскости. Угол между двумя плоскостями, условия параллельности и перпендикулярности двух плоскостей. Расстояние от точки до плоскости.

44.Прямая в пространстве. Различные виды уравнения прямой в пространстве. Угол между двумя прямыми в пространстве. Условие параллельности и перпендикулярности двух прямых.

45.Прямая и плоскость в пространстве. Угол между прямой и плоскостью. Условие параллельности и перпендикулярности прямой и плоскости. Пересечение прямой и плоскости. Условие принадлежности прямой плоскости.

46.Поверхности в пространстве. Цилиндрические поверхности. Поверхности вращения. Конические поверхности. Канонические уравнения поверхностей второго порядка и их изображения.

Составитель: доцент кафедры __________________/_Е. А.Сетько

Заведующий кафедрой __________________/_Е.А. Ровба