Каковы условия и особенности использования при разработке моделей систем дискретно-детерминированных моделей (F-схем)

Детерминированное моделирование отображает детерминированные процессы, т. е. процессы, в которых предполагается отсутствие всяких случайных воздействий. НДМ применимо там, где состояние система принимает состояния из некоторого набора по строго определенному закону, причем переход между состояниями осуществляется скачкообразно.

ДДМ являются предметом рассмотрения теории автоматов (ТА). ТА - раздел теоретической кибернетики, изучающей устройства, перерабатывающие дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени. Соответственно особенности применения ДДМ базируются на особенностях применения КА.

F- схема: F=<z,x,y,j,y,z₀>, (1)

где z,x,y - соответственно конечные множества входных, выходных сигналов (алфавитов) и конечное множество внутренних состояний (алфавита). z₀ÎZ - начальное состояние; j(z,x) - функция переходов; y(z,x) - функция выхода.

Автомат, построенный по такой схеме, и называется конечным и функционирует в дискретном автоматном времени, моментами которого являются такты, т.е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного, выходного сигнала и внутреннего состояния. Абстрактный автомат имеет один входной и один выходной каналы.

В момент t, будучи в состоянии z(t), автомат способен воспринять сигнал x(t) и выдать сигнал y(t)=y[z(t),x(t)], переходя в состояние z(t+1)=j[z(t),z(t)], z(t)ÎZ; y(t)ÎY; x(t)ÎX. Абстрактный КА в начальном состоянии z₀ принимая сигналы x(0), x(1), x(2) … выдаёт сигналы y(0), y(1), y(2)… (выходное слово).

Существуют F- автомат 1-ого рода (Миля), функционирующий по схеме:

z(t+1)= j[z(t),z(t)], t=0,1,2… (1)

y(t)=y[z(t),x(t)], t=0,1,2… (2)

F- автомат 2-ого рода:

z(t+1)= j[z(t),z(t)], t=0,1,2… (3)

y(t)=y[z(t),x(t-1)], t=1,2,3… (4)

Автомат 2-ого рода, для которого y(t)=y[z(t)], t=0,1,2,… (5)

т.е. функция выходов не зависит от входной переменной x(t), называется автоматом Мура.

Т.о. уравнения 1-5 полностью задающие F- автомат, являются частным случаем уравнения

(6)

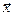где - вектор состояния, - вектор независимых входных переменных, - вектор воздействий внешней среды, - вектор собственных внутренних параметров системы, - вектор начального состояния, t - время; и уравнения

, (7)

когда система S - денорминированная и на её вход поступает дискретный сигнал x.