Дайте определение конечного автомата, укажите основные соотношения математической схемы конечного автомата

Конечный автомат имеет множество внутренних состояний и входных сигналов, являющихся конечными множествами. Автомат задаётся F- схемой:

F=<z,x,y,j,y,z₀>, (1)

где z,x,y - соответственно конечные множества входных, выходных сигналов (алфавитов) и конечное множество внутренних состояний (алфавита). z₀ÎZ - начальное состояние; j(z,x) - функция переходов; y(z,x) - функция выхода. Автомат функционирует в дискретном автоматном времени, моментами которого являются такты, т.е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного, выходного сигнала и внутреннего состояния. Абстрактный автомат имеет один входной и один выходной каналы.

В момент t, будучи в состоянии z(t), автомат способен воспринять сигнал x(t) и выдать сигнал y(t)=y[z(t),x(t)], переходя в состояние z(t+1)=j[z(t),z(t)], z(t)ÎZ; y(t)ÎY; x(t)ÎX. Абстрактный КА в начальном состоянии z₀ принимая сигналы x(0), x(1), x(2) … выдаёт сигналы y(0), y(1), y(2)… (выходное слово).

Существуют F- автомат 1-ого рода (Миля), функционирующий по схеме:

z(t+1)= j[z(t),z(t)], t=0,1,2… (1)

y(t)=y[z(t),x(t)], t=0,1,2… (2)

G- автомат 2-ого рода:

z(t+1)= j[z(t),z(t)], t=0,1,2… (3)

y(t)=y[z(t),x(t-1)], t=1,2,3… (4)

Автомат 2-ого рода, для которого y(t)=y[z(t)], t=0,1,2,… (5)

т.е. функция выходов не зависит от входной переменной x(t), называется автоматом Мура.

Т.о. уравнения 1-5 полностью задающие F- автомат, являются частным случаем уравнения

(6)

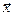где - вектор состояния, - вектор независимых входных переменных, - вектор воздействий внешней среды, - вектор собственных внутренних параметров системы, - вектор начального состояния, t - время; и уравнения

, (7)

когда система S - денорминированная и на её вход поступает дискретный сигнал x.

По числу состояний конечные автоматы бывают с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти (комбинационные или логические схемы) обладают лишь одним состоянием. При этом согласно (2), работа комбинационной схемы заключается в том, что она ставит в соответствие каждому входному сигналу x(t) определённый выходной сигнал y(t), т.е. реализует логическую функцию вида:

y(t)=y[x(t)], t=0,1,2,…

Эта функция называется булевой, если алфавиты X и Y, которым принадлежат значения сигналов x и y состоят из 2-х букв.

По характеру отсчёта времени (дискретному) F- автоматы делятся на синхронные и асинхронные. В синхронных автоматах моменты времени, в которые автомат "считывает" входные сигналы, определяются принудительно синхронизирующими сигналами. Реакция автомата на каждое значение входного сигнала заканчивается за один такт синхронизации. Асинхронный F- автомат считывает входной сигнал непрерывно и поэтому, реагируя на достаточно длинный водной сигнал постоянной величины x, он может, как это следует из 1-5, несколько раз изменить своё состояние, выдавая соответствующее число выходных сигналов, пока не перейдёт в устойчивое.

Для задания F- автомата необходимо описать все элементы множества F=<z,x,y,j,y,z₀>, т.е. входной, внутренний и выходной алфавиты, а также функции переходов и выходов. Для задания работы F- автоматов наиболее часто используются табличный, графический и матричный способ.