Дайте определение и приведите основные соотношения для моделирования разомкнутых систем массового обслуживания с очередями.

Системы массового обслуживания - это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания.

В СМО с очередями заявка, поступившая в систему в момент времени, когда свободен хотя бы один канал, обслуживается немедленно. Если же все каналы заняты, то поступившая заявка становится в очередь и ожидает обслуживания.

Рассмотрим несколько видов СМО с очередями:

1) Одноканальная СМО с неограниченной очередью.

Интенсивность поступления заявок равна λ. Интенсивность обслуживания заявок равна µ.

Уравнения Колмогорова для вероятностей состояний:

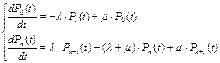
Стационарный режим функционирования данной СМО существует при t→ для любого n = 0, 1, 2, ... и когда λ<µ.

Решение системы имеет вид:

, при n = 0, 1, 2, ..., где .

Среднее число находящихся в системе заявок на обслуживание:

Средняя продолжительность пребывания заявки в системе:

Среднее число заявок в очереди на обслуживании:

Средняя продолжительность пребывания заявки в очереди:

.

2) Одноканальная СМО с ограниченной очередью.

Здесь независимо от того, сколько заявок поступает на вход обслуживающей системы, данная система не может вместить более N заявок, т.е. заявки, не попавшие в ожидание, вынуждены обслуживаться в другом месте.

Состояния СМО имеют следующую интерпретацию:

S₀ – «канал свободен»;

S₁ – «канал занят» (очереди нет);

S₂ – «канал занят» (одна заявка стоит в очереди);

…

S_n – «канал занят» (n-1 заявок стоит в очереди);

S_N – «канал занят» (N-1 заявок стоит в очереди).

Стационарное решение системы имеет вид:

, при n = 0, 1, 2, ..., N.

Вероятность отказа в обслуживании заявки:

Относительная пропускная способность:

Абсолютная пропускная способность:

Среднее число находящихся в системе заявок на обслуживание:

Средняя продолжительность пребывания заявки в системе:

Средняя продолжительность пребывания заявки в очереди:

Среднее число заявок в очереди на обслуживании:

.

3) Многоканальная СМО с неограниченной очередью.

Процесс массового обслуживания, описываемый данной моделью, характеризуется интенсивностью входного потока λ, при этом параллельно может обслуживаться не более S заявок. Средняя продолжительность обслуживания одной заявки равняется 1/µ.

Уравнения Колмогорова для вероятностей состояний:

Стационарный режим функционирования данной СМО существует при (ρ/S)<1.

Решение системы имеет вид:

, при n = 0, 1, 2, ...,.

Среднее число заявок в очереди на обслуживании:

Средняя продолжительность пребывания заявки в очереди:

.

Среднее число находящихся в системе заявок на обслуживание:

Средняя продолжительность пребывания заявки в системе: