Опишите, что представляют собой конгруэнтные процедуры генерации последовательностей

Конгруэнтные процедуры генерации.Широкое применение при моделировании систем на ЭВМ получили конгруэнтные процедуры генерации псевдослучайных последовательностей, представляющие собой арифметические операции, в основе которых лежит фундаментальное понятие конгруэнтности. Два целых числа а и b конгруэнтны (сравнимы) по модулю т, где т — целое число, тогда и только тогда, когда существует такое целое число к, что а—b=кт, т. е. если разность а.—b делится на т и если числа а и b дают одинаковые остатки от деления на абсолютную величину числа т. Например, 1984=4 (mod 10), 5008 = 8 (mod 10³) ит. д.

Конгруэнтные процедуры являются чисто детерминированными, так как описываются в виде рекуррентного соотношения, когда функция (4.9) имеет вид

где 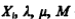— неотрицательные целые числа.

Раскроем рекуррентное соотношение :

(4.11)

Если заданы начальное значение Х₀, множитель λ и аддитивная константа µ, то (4.11) однозначно определяет последовательность целых чисел {X,}, составленную из остатков от деления на М членов последовательности Таким образом, для любого i>1 справедливо неравенство X_i<M. По целым числам последовательности { X_i } можно построить последовательность рациональных чисел из единичного интервала (0, 1). Конгруэнтная процедура получения последовательностей псевдослучайных квазиравномерно распределенных чисел может быть реализована мультипликативным либо сметанным методом.