Дайте определение и приведите основные соотношения для моделирования замкнутых систем массового обслуживания.

Замкнутой СМО называется такая СМО, у которой интенсивность поступления заявок λ зависит от состояния системы, причем источник заявок является внутренним и генерирует ограниченное число заявок.

Отличие от разомкнутой системы:

В разомкнутой системе интенсивность поступления заявок – это характеристика источника заявок. В замкнутой же системе потенциальное число заявок является величиной постоянной. После обслуживания заявки она снова возвращается в источник. Поэтому в замкнутой системе интенсивность поступления заявок является характеристикой конкретно объекта, поступающего в систему.

Пример:

Пусть в машинном парке имеется N машин и M механиков, которые чинят эти машины, когда они сломаются, причем N>M и каждая машина может обслуживаться только одним механиком. Здесь машина – это заявка, а механик – канал обслуживания. Неисправная машина после обслуживания снова вводится в эксплуатацию и становится потенциальной заявкой.

Интенсивность λ зависит от того, сколько машин в данный момент находится в эксплуатации (N-k) и сколько машин обслуживается или стоит в очереди, ожидая обслуживания (k).

Заявка, поступившая в систему в момент времени, когда свободен хотя бы один канал, обслуживается немедленно. Если же все каналы заняты, то поступившая заявка встает в очередь.

Состояние S_k системы характеризуется общим числом заявок, находящихся на обслуживании и в очереди, равным k. При этом если система находится в состоянии S_k, то число объектов, находящихся в эксплуатации, равно (N-k).

Если λ – интенсивность потока требований в расчете на одну машину, то:

Система алгебраических уравнений, описывающих работу замкнутой СМО в стационарном режиме, выглядит следующим образом:

Решая данную систему, находим вероятность k-гo состояния:

Среднее число заявок в очереди на обслуживании:

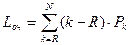
Среднее число находящихся в системе заявок на обслуживание:

Среднее число механиков (каналов), «простаивающих» из-за отсутствия работы:

Коэффициент простоя обслуживаемого объекта (машины) в очереди:

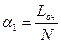
Коэффициент использования объектов (машин):

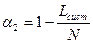
Коэффициент простоя обслуживающих каналов (механиков):

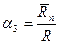
Средняя продолжительность пребывания заявки в очереди:

.