Опишите процесс решения задачи линейного программирования симплекс-методом

Линейное программирование первоначально развивалось как направление, разрабатывающее новые подходы к решению задач минимизации выпуклых функций, т. е. в рамках выпуклого программирования. Выпуклое программирование посвящено нахождению экстремума выпуклой целевой функции на выпуклом множестве, обычно задаваемом в виде системы выпуклых неравенств.

Пусть мы имеем задачу линейного программирования:

Целевая функция вида:

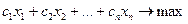
и ограничения

,

Переобозначим свободные коэффициенты ограничений a_j0=b_j. Приведем матрицу ограничений к каноническому виду:

Используя метод Жордана-Гаусса, приведем записанную систему к виду, где выделены базисные переменные. Введем условные обозначения:

x₁, x₂ , ... , x_r - базисные переменные;

x_r+1, x_r+2 , ... , x_n - свободные переменные.

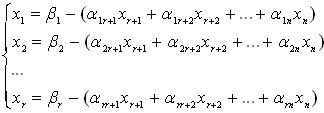; . (2.41)

По последней системе ограничений и целевой функции построим симплекс-таблицу.

Таблица 2.3

Симплекс-таблица

Все дальнейшие преобразования связаны с изменением содержания этой таблицы.

Нижняя строка элементов а_ок, называется индексной. Элементы индексной строки вычисляются следующим образом:

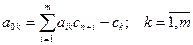означает номер соответствующей строки.

Поскольку на первом шаге заполнения таблицы все элементы с_n+I равны нулю, то элементам индексной строки присваиваются значения со­ответствующих элементов целевой функции данного столбца, взятые с обратным знаком, т.е. а_0k= -С_к. Последняя строка таблицы служит для определения направляющего столбца.

Элемент а₀₀ равен значению целевой функции, которое вычисляется по формуле , к - номер базисной переменной (индексация идет по строкам таблицы).

В столбце В_х записываются базисные переменные, на первом шаге в качестве базисных выбирают фиктивные переменные {х_п+к }, . В дальнейшем фиктивные переменные необходимо вывести из базиса.

В столбец С записываются коэффициенты при х_п+к, на первом шаге значения этих коэффициентов равны нулю.

Для перехода от базиса фиктивных переменных к базису реальных переменных применяют следующие правила:

* в качестве направляющего столбца выбирают столбец А_j , для которого выполняется условие a_0j = min{a_ol), при а_0l < 0, т.е. выбирается минимальный элемент, при условии, что этот элемент отрицательный;

* выбирают направляющую строку, для чего каждый элемент столбца свободных членов делится на соответствующий элемент направляющего столбца, элемент столбца свободных членов находится в одной строке с элементом направляющего столбца -. Из всех возможных соотношений выбирается минимальное при условии, что a_rj > 0, 1 ≤ r ≤ т.

Применяя сформулированные правила, определяем направляющий элемент. Далее выполняется шаг симплексных преобразований.

Переменная, которая соответствует направляющему столбцу, вводится в базис, а переменная, соответствующая направляющей строке, выводится из базиса. При этом для переменной, вводимой в базис, изменяется соответствующее значение коэффициента целевой функции. Вместо коэффициента с_n+i соответствующего старой базисной переменной, в таблице записывается значение коэффициента целевой функции при переменной, вводимой в базис.

Если направляющий элемент а_ij, то переход от данной таблицы к следующей осуществляется с использованием следующих правил.

1. Для всех элементов направляющей строки

где к - номер шага (к = 1, 2,...); i - номер направляющей строки; j - номер направляющего столбца; , т.е. все элементы направляющей строки делим на направляющий элемент, в итоге направляющий элемент стал равным единице; .

2. В направляющем столбце необходимо получить , для всех , r≠i, при , т.е. в направляющем столбце должны быть все нули кроме направляющего элемента, который равен единице.

Для всех остальных элементов, включая индексную строку, производим вычисления

Симплексные преобразования повторяют до тех пор, пока не реализуется один из двух возможных исходов:

а) все a_0l ≥0 - это условие оптимальности базиса последней таблицы;

б) найдется такой элемент a_0l< 0, при котором все элементы столбца а_rj ≤ 0, - это признак неограниченности целевой функции на множестве допустимых решений.