Рассмотрите пример решения задачи линейного программирования симплекс-методом

Пример решения задачи линейного программирования.Рассмотрим задачу линейного программирования в следующем виде: найти максимум линейной формы 4х₁ + 3х₂ при ограничениях

х₁ ≤4000, х₂ ≤ 6000, х₁ +2/3х₂ ≤6000, х_1,х₂ ≥ 0.

Каноническая форма задачи линейного программирования будет иметь вид

4x₁ + 3x₂ + 0x₃ + 0x₄ + 0x₅ → max;

1х₁ + 0х₂ + 1х₃ + 0x₄ +0x₅ = 4000;

0x₁ +1х₂ +0 х₃ +1 x₄+0 x₅ = 6000;

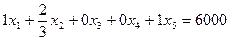
Составим исходную симплекс-таблицу (табл. 10.2).

Таблица 10.2

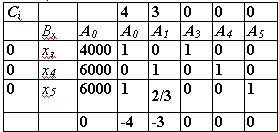
Поскольку -4 < -3 < 0, то в качестве направляющего выбираем первый столбец. Составив отношение вида , определяем направляющую строку, Для этого находим минимальное отношение

Следовательно, направляющая строка - первая, направляющий элемент — а₁₁=1. Применив первый шаг симплексного преобразования, получим новую таблицу (табл. 10.3).

Таблица 10.3

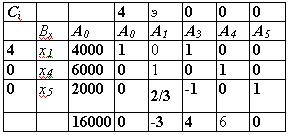
На данном этапе в качестве направляющего столбца выбираем второй, направляющая строка - третья, т.к.

Применим следующий шаг симплексного преобразования. В результате получим табл. 10.4

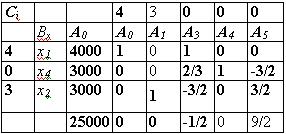
Так как 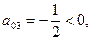то направляющий столбец А₃, направляющая строка - вторая, направляющий элемент а₂₃= 3/2 • Выполним очередной шаг преобразования, получим еще одну таблицу (табл. 10.5).

Таблица 10.5

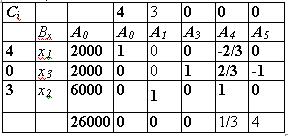
Поскольку в индексной строке все элементы положительны, это означает, что найдено оптимальное решение х₁₀= 2000, х₂₀ = 6000, х₃₀ = 2000. Искомое значение целевой функции равно 4 х₁ + Зх₂= 26000.