Дайте общую математическую формулировку задач нелинейного программирования

Математическое программирование подразделяется на линейное, целочисленное, нелинейное, динамическое программирование.

Нелинейное программирование- раздел теории оптимизации (теории экстремальных задач), посвященный исследованию и решению задач минимизации (максимизации), в которых целевая функция и ограничения не являются линейными.

В общем виде задачу нелинейного программирования можно сформулировать так:

F(х)→min (max) (Ш.1)

при условии

g(x)≤ 0, (Ш.2)

где х - вектор искомых переменных; F (х) - целевая числовая функция; g(x) - вектор-функция системы ограничений.

В отличие от линейного программирования теория экстремальных задач, в которой целевая функция и/или функции, задающие ограничения, не линейны, называется нелинейным программированием. В частности, таковым является квадратичное программирование, в котором изучается задача нахождения экстремума квадратичной функции при линейных ограничениях типа равенств и/или неравенств.

При этом могут быть разные случаи: целевая функция - нелинейная, а ограничения - линейны; целевая функция - линейная, а ограничения (хотя бы одно из них) - нелинейные; целевая функция и ограничения нелинейные. Задачи условной оптимизации нелинейного программирования бывают двух типов: когда в ограничениях (2) имеют место а) знаки равенства б) знаки неравенства.

Решение задачи нелинейного программирования (поиск глобального минимума или максимума) состоит в отыскании таких значений переменных, подчиненных системе ограничений, при которых достигает минимума или максимума данная целевая функция.

Задачи нелинейной оптимизации с точки зрения методов решения делятся на два класса: 1) задачи безусловной оптимизации; 2) задачи условной оптимизации.

Задача безусловной оптимизации представляет собой поиск оптимума целевой функции без всяких дополнительных условий, что записывается

.

Задача условной оптимизации в общем случае записывается в известном виде:

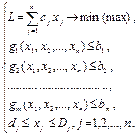
51.Поясните понятия: задача многокритериальной оптимизации, множество допустимых решений, оптимальное решение. Дайте общую математическую формулировку задач многокритериальной оптимизации

В задачах, которые были рассмотрены до сих пор, был только один критерий оптимальности, одна цель, однако зачастую свести задачу к одному критерию достаточно трудно, так как целей может быть много. В этом случае оптимизацию производят по нескольким частным критериям , а полученные задачи называют задачами многокритериальной или векторной оптимизации. Многокритериальная оптимизация представляет собой попытку получить наилучшее значение для некоторого множества характеристик рассматриваемого объекта, то есть найти некоторый компромисс между теми частными критериями , по которым требуется оптимизировать решение.

Постановку задачи можно представить следующим образом:

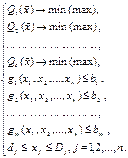
Оптимальное решение - это решение, которое с точки зрения лица, принимающего решение, предпочтительнее других возможных решений. Таким образом, понятие оптимального решения связано с предпочтениями лица, принимающего решение. Эти предпочтения на практике выражаются в различной форме, и их математическая формализация может составить сложную задачу, поскольку лицо, принимающее решение, как правило, не может ясно и четко сформулировать их.

Цель теории принятия решений и состоит в разработке методов, которые помогли бы лицу, принимающему решение, наиболее полно и точно выразить свои предпочтения в рамках соответствующей математической модели и в конечном счете обоснованно выбрать действительно оптимальное решение.

Множество допустимых решений (МДР) - пространство решения. Так называется область, определяемая всеми проектными параметрами. Пространство решения не столь велико, как может показаться, поскольку оно обычно ограничено рядом условий, связанных с физической сущностью задачи. Ограничения могут быть столь сильными, что задача не будет иметь ни одного удовлетворительного решения. Следует отметить, что очень часто в связи с ограничениями оптимальное значение целевой функции достигается на одной из границ области множества допустимых решений задачи.