ОДУ n-го порядка, разрешённое относительно старшей производной

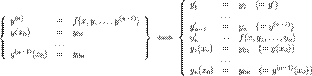
Теоремы о разрешимости задачи Коши для ОДУ

Пусть в области 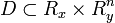рассматривается задача Коши:

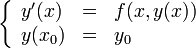
где 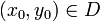. Пусть правая часть является непрерывной функцией в . В этих предположениях имеет место теорема Пеано, устанавливающая локальную разрешимость задачи Коши: Пусть a>0 и b>0 таковы, что замкнутый прямоугольник

принадлежит области D, тогда на отрезке [x₀ − α,x₀ + α], где α = min{a,b / M}, 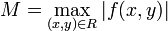, существует решение задачи Коши.

Указанный отрезок называется отрезком Пеано. Заметим, что, локальный характер теоремы Пеано не зависит от гладкости правой части. Например, для f(x,y) = y² + 1 и для x₀ = 0,y₀ = 0 решение y(x) = tan(x) существует лишь на интервале ( − π,π). Также отметим, что без дополнительных предположений относительно гладкости правой части, нельзя гарантировать единственность решения задачи Коши. Например, для возможно более одного решения.

Чтобы сформулировать теорему о единственности решения задачи Коши, необходимо наложить дополнительные ограничения на правую часть. Будем говорить, что функция f(x,y) удоволетворяет условию Липшица на D относительно y, если существует постоянная L такая, что

для всех , i=1,2.

Пусть правая часть f(x,y) дополнительно удовлетворяет условию Липшица на D относительно y, тогда задача Коши не может иметь в D более одного решения.

Также отметим, что хотя эта теорема имеет глобальный характер, тем не менее она не устанавливает существование глобального решения.

Для существования глобального решения необходимо наложить условия на рост правой части по y: пусть функция f удовлетворяет условию

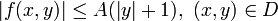
где A>0 - константа не зависящая ни от x, ни от y, тогда задача Коши имеет решение в D. В частности, из этой теоремы следует, что задача Коши для линейных уравнений (с непрерывными по x коэффициентами) имеет глобальное решение.

Вычислительные (численные) методы — методы решения математических задач в численном виде

Представление как исходных данных в задаче, так и её решения — в виде числа или набора чисел

В системе подготовки инженеров технических специальностей является важной составляющей.

Основами для вычислительных методов являются:

решение систем линейных уравнений

интерполирование

численное интегрирование

численное решение системы нелинейных уравнений

численное решение обыкновенных дифференциальных уравнений

Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление»^. Метод Эйлера является явным, одношаговым методом первого порядка точности, основанном на аппроксимации интегральной кривой кусочно линейной функцией, т. н. ломаной Эйлера.

Описание метода

Пусть дана задача Коши для уравнения первого порядка

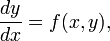
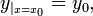
где функция f определена на некоторой области . Решение разыскивается на интервале (x₀,b]. На этом интервале введем узлы

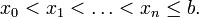
Приближенное решение в узлах x_i, которое обозначим через y_i определяется по формуле

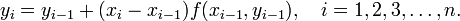
Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.

Оценка погрешности

Метод Эйлера является методом первого порядка. Если функция f непрерывна в D и непрерывно дифференцируема по переменной y в D, то имеет место следующая оценка погрешности

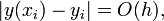
где h — средний шаг, то есть существует C > 0 такая, что .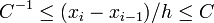

Заметим, что условия гладкости на правую часть, гарантирующие единственность решения задачи Коши, необходимы для обоснования сходимости метода Эйлера.

Значение метода Эйлера

Метод Эйлера являлся исторически первым методом численного решения задачи Коши. О. Коши использовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит свое применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.

Модифицированный метод Эйлера с пересчетом

Вычисления по методу Эйлера с пересчетом делаются в два этапа.

Прогноз:

.

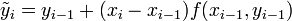Коррекция:

.

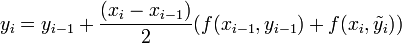Модифицированный метод Эйлера с пересчетом имеет второй порядок точности, однако для его реализации необходимо дважды вычислять правую часть функции. Заметим, что метод Эйлера с пересчетом представляет собой разновидность методов Рунге-Кутты (предиктор-корректор).

3. Указать к какому классу относится каждый из перечисленных IP адресов:

192.168.0.15

127.0.0.1

112.0.0.15

167.58.13.21

Определить к какому классу относится каждый IP-адрес

Старший октет адреса представляем в двоичном коде: если старший бит = 0 (класс А), = 10 (класс B), = 11 (класс С)

192.168.0.15

Ответ: Класс С

127.0.0.1

Ответ: Класс А

112.0.0.15

Ответ: Класс А

167.58.13.21

Ответ: Класс В