Промежуточная область (область Френеля).

При расстояниях R<2D²/λ дальняя зона излучающей системы плавно переходит в промежуточную область, иногда называемую областью Френеля. При расчете полей излучающих систем в про­межуточной области делаются следующие упрощения:

1. Как и в случае дальней зоны, величина r в знаменателе подынтегрального выражения (7.1) принимается приближенно рав­ной R и выносится из-под знака интеграла.

2. В показателе экспоненты подынтегральной функции в (7.1) принимается, r≈R-R^’cosα+R^’2(1-cos²α)/(2R), что соответст­вует отбрасыванию в степенном ряду членов выше второй сте­пени. Функция ехр(-jβR), не зависящая от координат источников, выносится из-под интеграла.

Таким образом, в промежуточной области векторные потенциалы определяются по формуле

3. При выполнении операций пространственного дифференцирования отбрасываются все члены, имеющие радиальную зависимость 1/R² и 1/R³, аналогично тому, как эго де­лалось при вычислении полей дальней зоны.

Компоненты векторов поля Е и Н в промежуточной области могут быть найдены с заменой в них векторных потенциа­лов A_∞^эм на векторные потенциалы А_фр^ЭМ.

Поперечный характер поля его локальное подобие плоской ЭМ волны сохраняется, но зависимость поля от расстояния не имеет характера сферической волны. Расчеты показывают, что на монотонное убывание поля по закону 1/R накладывается осциллирующее затухающее колебание.

Чем меньше расстояние R тем сильнее искажается диаграмма направленности анализ показывает, что пределы зоны определяются как 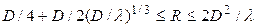, т.е. при размере D=10λ параметры будут 13,5≤R≤200λ.