Відносний спокій рідини

2.4.1 При русі резервуару в горизонтальному напрямку з постійним прискоренням (рис. 2.6) на рідину, що перебуває в ньому, діє сила ваги й сила інерції. Вільна поверхня являє собою похилу поверхню, рівняння якої має вид

, (2.19)

де С – постійна величина;

а – прискорення резервуару.

Гідростатичний тиск у будь-якій точці рідини

, (2.20)

де h – відстань по вертикалі від точки до вільної поверхні.

П’єзометрична поверхня П – П, проходить паралельно вільної поверхні на висоті

,

якщо тиск на вільній поверхні р₀ > р_атм (рис. 2.6), або на глибині

,

під вільною поверхнею рідини, якщо р₀ < р_атм.

Рисунок 2.6

Сила тиску на передню (задню) плоску стінку

, (2.21)

де h'_c й h_c – відстані по вертикалі від центра ваги стінки до вільної поверхні рідини та до п’єзометричної поверхні відповідно.

Силу тиску на криволінійну площину (рис. 2.7) може бути знайдено з умови динамічної рівноваги об’єму рідини V, що міститься між криволінійною площиною й поверхнею, проведеною через граничний контур об’єму рідини (на рис. 2.7 цей об’єм заштрихований):

, (2.22)

де Р₁ – сила тиску на плоский переріз АВ, визначена за формулою (2.21);

F = r∙ a∙ V – сила інерції, що діє на заштрихований об’єм рідини;

G = r∙ g∙ V – вага цього об’єму рідини.

Рисунок 2.7

2.4.2 При обертанні резервуару навколо вертикальної осі z (рис. 2.8) на будь-яку частку M рідини крім сили ваги діє також відцентрова сила інерції

Рисунок 2.8

, (2.23)

яку можна розкласти на дві складові

, , (2.24)

де m – маса частки;

ω – кутова швидкість;

r – відстань від частки до осі обертання;

х и у – проекції вектора r на координатні осі, причому х² + у² = r².

Отже, проекції прискорення масових сил на координатні осі в розглянутому випадку рівноваги рідини рівні

, , .

Підставивши ці значення X, Y, і Z в диференціальне рівняння рівноваги (2.1) і виконавши інтегрування, одержимо

, (2.25)

де р₀ – тиск на вільній поверхні; z₀ – вершина параболоїда обертання.

У довільній точці, розташованій на глибині h під поверхнею рідини, тиск

. (2.26)

Поверхні рівня являють собою параболоїди обертання. Рівняння вільної поверхні рідини має вигляд

. (2.27)

П’єзометрична поверхня при р₀ = р_атм збігається з вільною поверхнею рідини. Якщо вільна поверхня відсутня (закритий резервуар повністю заповнений рідиною під тиском), то п’єзометрична поверхня проходить через точку рідини, у якій тиск дорівнює атмосферному (наприклад, через рівень у відритому п’єзометрі , де р₀ = р_атм).

Якщо R – радіус резервуару, а ω - кутова швидкість, то висота параболоїда обертання

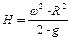. (2.28)

Об’єм параболоїда обертання

. (2.29)