Рівняння Бернуллі

При рішенні деяких найпростіших завдань про рух рідин часто в першому наближенні роблять допущення про те, що рідина, що рухається, є ідеальною. Під ідеальною розуміють рідину абсолютно нестисливу яка не розширюється, не здатну чинити опір розтяганню й зсуву. Головне, чим відрізняється рідина ідеальна від рідини реальної - це відсутність у неї в'язкості, що викликає здатність чинити опір зсуву, тобто виникненню дотичних напружень (тертя в рідині).

Отже, в ідеальній рідині, що рухається, можливий лише один вид напруги - напруга стиску, тобто тиск р, а дотичне напруження τ = 0.

Основними рівняннями, що дозволяють вирішувати найпростіші задачі про рух ідеальної рідини, є рівняння витрати й рівняння Бернуллі.

Рівняння Бернуллі для потоку ідеальної рідини виражає собою закон збереження питомої енергії рідини уздовж потоку. Під питомою розуміють енергію, віднесену до одиниці ваги, об’єму або маси рідини. Звичайно зручніше буває відносити енергію до одиниці ваги. У цьому випадку рівняння Бернуллі, що записане для двох перерізів елементарної струминки або потоку ідеальної рідини, має вигляд

. (3.8)

Для двох перерізів потоку реальної (в'язкої) рідини при усталеному русі, що плавно змінюється, рівняння Бернуллі має вигляд

, (3.9)

де й₁ (υ₁) і й₂ (υ₂) – дійсні (середні) швидкості відповідно в першому та у другому перерізах;

р₁ і р₂ – тиск рідини відповідно у першому та другому перерізах;

z₁й z₂ – відстані від довільної горизонтальної поверхні порівняння до центрів перерізів;

– сумарні втрати повного напору між перерізами.

З геометричної точки зору, складові рівняння Бернуллі являють собою наступне:

z – висоту, на якій розташовується центр живого перерізу над поверхнею порівняння О-О;

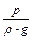– п’єзометричну висоту, яку можна виміряти п’єзометричною трубкою;

– висоту швидкісного напору, що дорівнює різниці рівнів у трубках повного й статичного напорів.

Суму висот – називають повним гідродинамічним напором.

Коефіцієнт α являє собою відношення дійсної кінетичної енергії до кінетичної енергії, підрахованої по середній швидкості. При турбулентному режимі руху α ≈ 1, при ламінарному в круглій трубі α = 2.

За допомогою рівняння Бернуллі (3.9) розв’язується багато задач практичної гідравліки. Для цього вибираються два перерізи потоку так, щоб в одному з них величини z, p й υбули відомі, а в другому невідомою була лише одна величина. Потім вибирається горизонтальна поверхня порівняння. Її доцільно провести через центр одного з обраних перерізів, тоді z₁ або z₂ буде рівним нулю. Після спрощення рівняння Бернуллі, записаного для обраних перерізів, знаходять невідому величину (p, υ або z).