
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Характеристика центробежного насоса
Рабочие органы насоса рассчитывают для определенного сочетания подачи, напора и частоты вращения, причем размеры и форму проточной полости выбирают так, чтобы гидравлические потери при работе на этом режиме были минимальными. Такое сочетание подачи, напора и частоты вращения называется расчетным режимом. При эксплуатации насос может работать на режимах, отличных от расчетного. Так, прикрывая задвижку, установленную на напорном трубопроводе насоса, уменьшают подачу. При этом также изменяется напор, развиваемый насосом. Для правильной эксплуатации насоса необходимо знать, как изменяются напор, КПД и мощность, потребляемая насосом, при изменении его подачи, т. е. знать характеристику насоса, под которой понимается зависимость напора, мощности и КПД от подачи насоса при постоянной частоте вращения.
Ограничимся рассмотрением случая подвода жидкости к рабочему колесу без момента скорости (υu1=0). При этом теоретический напор при бесконечном числе лопаток, согласно уравнению (5.27)
HТ∞= (ω/g)υu2∞R2=u2υu2∞/g (5.30)
Из треугольника скоростей на выходе из рабочего колеса (см. рис. 5.10) и уравнения (5.24) находим
υu2∞=u2- υm2 ctg β2л=u2 – ctg β2л Qk/(2πR2b2ψ2) (5.31)
Подставив это выражение в уравнение (5.30),получим
Нт∞=u22/g – u2ctgβ2лQk/ (g2πR2b2ψ2) (5.32)
Из уравнения следует, что зависимость теоретического напора при бесконечном числе лопаток от расхода Qk через колесо линейная (рис. 5.11). При подаче, равной нулю (задвижка на напорном трубопроводе закрыта полностью),
HТ∞= u22/g.
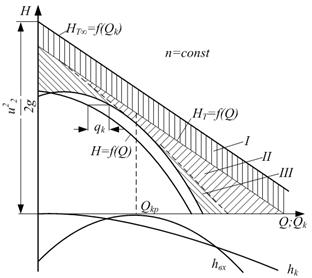
Рис. 5.11. Характеристика центробежного насоса:
I – уменьшение напора из-за конечного числа лопаток; II – потери в каналах насоса hk; III – потери на входе в рабочее колесо и отвод hвх
При конечном числе лопаток зависимость теоретического напора НТ от расхода через рабочее колесо тоже линейная. Так как на одинаковых подачах теоретический напор при конечном числе лопаток меньше, чем при бесконечном, прямая НТ=f (Qk) расположена ниже прямой HТ∞=f(Qk). Из уравнений (5.26) и (5.13) следует, что приближенно прямые HТ∞=f(Qk) и НТ=f (Qk) параллельны.
Напор, развиваемый насосом, меньше теоретического на величину гидравлических потерь:
Н=НТ - hп.
Эти потери состоят из потерь hвх при входе в рабочее колесо и в отвод и потерь hk в каналах подвода, рабочего колеса и отвода (потери в каналах насоса).
Потери в каналах насоса приближенно пропорциональны скорости жидкости во второй степени и, следовательно, расходу во второй степени:
Hk= kQ2k ,
где k - сопротивление каналов.
На рис. 5.11 изображена ниже оси абсцисс кривая hк = f (Qk), являющейся параболой с вершиной в начале координат.
Рассмотрим потери при входе в рабочее колесо. На рис. 5.12, а изображен треугольник АВС скоростей входа при расчетном режиме. Поскольку рассматриваем случай отсутствия закрутки на входе в рабочее колесо (υu1=0), треугольник скоростей является прямоугольным. Направление входного элемента лопатки при расчетном режиме выбираем близким к направлению относительной скорости, жидкости ω1р. Следовательно, при расчетном, режиме β1р=β1л и потери на входе в рабочее колесо практически отсутствуют. При уменьшении подачи меридиональная скорость уменьшается. Направление абсолютной скорости определяется конструкцией подвода и от подачи не зависит, поэтому в данном случае закрутка потока на входе равна нулю независимо от подачи (υu1= 0). Таким образом, при уменьшении подачи получаем треугольник ABС скоростей. Из рис. 5.12, а видно, что при нерасчетной подаче направление относительной скорости ω1 не совпадает с направлением входного элемента лопатки (β1=β1л). При этом поток отрывается от лопатки и образуется вихревая зона (рис. 5.12, б), наличие которой ведет к дополнительным потерям энергии.

Рис. 5.12. Треугольники скоростей на входе в рабочее колесо
при различных режимах работы насоса
Причина потерь у входа в отвод следующая. Сечения отвода рассчитывают так, чтобы при расчетном режиме момент скорости жидкости в отводе был равен моменту скорости на выходе из рабочего колеса. При этом никакого изменения скоростей у входа в отвод нет, и потери при входе равны нулю. При уменьшении подачи насоса через то же сечение отвода проходит меньший расход жидкости. Следовательно, скорости в отводе и их момент при уменьшении подачи уменьшаются пропорционально последней, скорости же на выходе из рабочего колеса возрастают. Для бесконечного числа лопаток это хорошо видно из рис. 5.13. То же получается и при конечном числе лопаток. Таким образом, при подачах, меньших расчетной, момент скорости жидкости на выходе из рабочего колеса больше, чем в отводе. Аналогично при подачах, больших расчетной, момент скорости жидкости в отводе больше, чем на выходе из рабочего колеса.
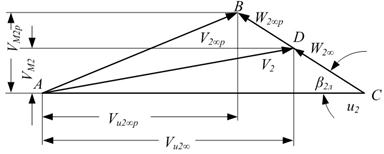
Рис. 5.13. Треугольники скоростей на выходе из рабочего колеса при различных режимах работы насоса
Следовательно, при подачах, отличных от расчетной, потоки вытекающей из рабочего колеса и текущей по отводу жидкости имеют разные моменты скорости. При слиянии этих потоков в отводе наблюдаются вихреобразование и дополнительные потери.
На рис. 5.11 ниже оси абсцисс изображена кривая hвх=f(Qk). При расчетном расходе QКР потери как у входа в рабочее колесо, так и у входа в отвод равны нулю. При отклонении подачи от расчетной эти потери быстро увеличиваются. Вычтя из ординат линии HТ = f(Qk) ординаты кривых потерь в каналах насоса и у входа в рабочее колесо и в отвод, получим кривую Н = f (Qк) зависимости напора насоса от расхода жидкости через колесо.
Подача насоса отличается от расхода через рабочее колесо на величину утечек:
Q= Qк - qk.
Из уравнения (5.13) следует, что теоретический напор не зависит от рода жидкости [в уравнении (5.13) отсутствуют величины, характеризующие физические свойства жидкости]. Гидравлические потери являются функцией Rе и, следовательно, зависят от вязкости жидкости. Однако, если Rе велико и имеет место турбулентная автомодельность потоков в рабочих органах насоса, то гидравлические потери и, следовательно, напор насоса от рода жидкости не зависят, поэтому график напоров характеристики лопастного насоса одинаков для разных жидкостей, если потоки в рабочих органах насоса автомодельны.
Построим кривую мощности. Из уравнения (5.6) гидравлическая мощность
NГ =QkρgHт
Зависимость теоретического напора Нтот расхода через рабочее колесо линейна (см. рис. 5.11) и может быть выражена уравнением
НТ= А-ВQk.
Отсюда гидравлическая мощность
NГ=ρg(AQk-BQ2k)
Это уравнение является уравнением параболы, пересекающей ось абсцисс в точках Qк = 0 и Qk = А/В рис. 5.14, кривая NГ = f(Qk).

Рис. 5.14. Характеристика центробежного насоса,
полученная теоретически
Механические потери мало зависят от подачи насоса. Прибавив мощность механических потерь к гидравлической мощности, получаем кривую N = f(Qk) зависимости мощности на валу насоса от расхода жидкости через рабочее колесо. Для получения кривой мощности характеристики насоса остается учесть объемные потери, при этом кривую N =f(Qk) надо сместить влево на величину утечек qк.
Имея кривые N = f(Qk) и Н = f (Q),построим кривую КПД по уравнению
ŋ = QρgH/N .
При Q = 0 и H = 0, ŋ = 0. Следовательно, кривая КПД пересекает ось абсцисс в начале координат (Q = 0) и в точке, где ее пересекает кривая напора.
Приведённые выше рассуждения являются приближёнными, так как не учитывают ряда факторов, влияющих на напор и мощность. В частности, они не учитывают вторичных токов, возникающих при малых подачах, неустановившиеся движения жидкости в каналах колеса при нерасчётных режимах и т.д. Поэтому характеристика насоса, построенная теоретически на основании описанных рассуждений, плохо согласуется с данными опыта. Характеристика насоса может быть получена лишь опытным путём.
На рис. 5.15. изображена характеристика центробежного насоса. На ней нанесены кривые зависимости напора Н, мощности N, КПД η и допустимого кавитационного запаса ∆hдоп (см. п. 5.19) от подачи Q.
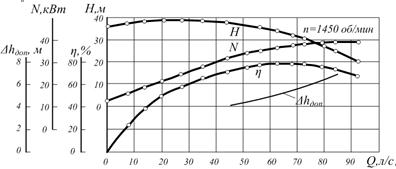
Рис. 5.15. Характеристика центробежного насоса, полученная экспериментально
Дата добавления: 2015-04-18; просмотров: 268; Мы поможем в написании вашей работы!; Нарушение авторских прав |