Решение. Найдем силу давления воды на стенку слева

Координата центра давления

l_D1 = l_т + J/l_т s.

Для прямоугольной стенки J = , тогда

м.

Точно так же справа:

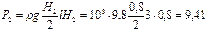кН,

м.

Опрокидывающий момент, т.е. момент сил давления жидкости относительно точки О (см. рис. 5.1.12):

Н·м.

Устойчивость против опрокидывания сообщает стенке момент силы тяжести относительно точки О:

Н·м.

Так как М_тяж > М_опр, то стенка устойчива.

Пример 8.1.5. Для слива жидкости из бензохранилищ имеется квадратный патрубок со стороной h = 0,3 м, закрытый крышкой, шарнирно закрепленной в точке О. Крышка опирается на торец патрубка и расположена под углом 45° (α = 45°) к горизонту (рис. 8.5).

Определить (без учета трения в шарнире О и рамке В) силу F натяжения троса, необходимую для открытия крышки АО, если уровень бензина Н = 3 м, давление над ним, измеренное манометром, р_м = 5 кПа, а плотность бензина ρ = 700 кг/м³ . Вес крышки не учитывать.

Рис. 8.5. Кпримеру 8.1.5

Решение

Найдем силу давления на стенку АО. Рассматриваемой смоченной поверхностью является прямоугольная наклонная стенка высотой h/sin α ишириной h, т.е. s = h ²/sin α.

Центр тяжести этой стенки находится на глубине h _т = H - h/2, Δр = р_м, т.е.

кН.

Найдем теперь расстояние между центром давления и центром тя­жести крышки.

м.

Тогда

м.

Момент инерции прямоугольной стенки относительно горизонталь­ной оси, проходящей через центр тяжести стенки:

Тогда

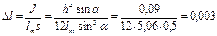м.

Найдем силу натяжения троса из уравнения моментов сил, взятых относительно оси шарнира О:

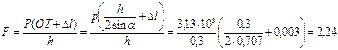кН.