
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ДВИЖЕНИЕ ГАЗА ПО ТРУБАМ
В промышленности и коммунальном хозяйстве весьма широко применяется (для различных технических и бытовых целей) перекачка по трубам газообразных жидкостей — газов, воздуха и перегретого пара. Транспортировка этих жидкостей (в дальнейшем сокращенно называемых просто газами) по трубопроводам, по сравнению с движением обычных капельных жидкостей, характеризуется рядом существенных особенностей, обусловливаемых различиями физических свойств капельных и газообразных жидкостей,
Для иллюстрации методики расчета газопроводов рассмотрим часто встречающийся случай движения газа по трубопроводу постоянного поперечного сечения. При движении газа по такому трубопроводу вследствие неизбежных потерь напора давление газа, обычно превышающее атмосферное давление в начальном сечении, по длине трубопровода непрерывно снижается. При этом происходит расширение газа — удельный объем газа увеличивается, а его плотность, наоборот, уменьшается; указанное изменение плотности газа, в отличие от случая капельных жидкостей, оказывается весьма существенным и должно обязательно учитываться при расчете.
В случае установившегося движения массовое количество газа, проходящего через любое поперечное сечение трубопровода в единицу времени (массовый расход газа т), вследствие неразрывности
движения остается неизменным; объемный же расход газа Q = 
будет увеличиваться, а следовательно, будет возрастать по длине трубопровода и средняя скорость течения газа
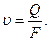
В общем случае вследствие расширения газа и явления теплообмена будет иметь место также и непрерывное изменение температуры газа по длине трубопровода. Однако в ряде случаев с достаточной для практических расчетов точностью оказывается вполне возможным принять температуру постоянной, считая, что процесс расширения газа происходит изотермически.
При изотермическом процессе ввиду постоянства температуры будет сохранять постоянное значение по длине трубопровода также и абсолютная вязкость газа . При этом, как нетрудно убедиться, останется постоянным и число Рейнольдса.
В самом деле,
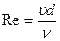
но так как
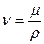 ,
, 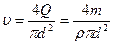 ,
,
то число Рейнольдса можно представить также в виде
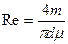
В правую часть полученного выражения входят лишь такие величины, которые сохраняют постоянное значение по длине трубопровода; следовательно, постоянным по длине трубопровода будет и число Рейнольдса, а следовательно, и коэффициент гидравлического сопротивления X, являющийся функцией этого числа.
Исходным уравнением для определения падения давления и расхода газа в газопроводе является обычное уравнение Бернулли. Однако, учитывая отмеченные выше особенности, наблюдающиеся при движении газа в газопроводе (изменение плотности газа и средней скорости его течения по длине газопровода), это уравнение в рассматриваемом случае необходимо писать в дифференциальной форме
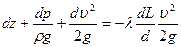 ,
,
или
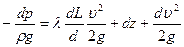 (6.36)
(6.36)
Подсчеты показывают, что второй и третий члены правой части этого уравнения в обычных на практике условиях движения газов (при горизонтальном расположении трубопровода, и малых дозвуковых скоростях течения) оказываются малыми по сравнению с первым членом, учитывающим сопротивление движению, и поэтому ими можно пренебречь. Тогда вместо уравнения (6.36) будем иметь
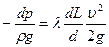 .
.
Выражая далее среднюю скорость течения газа через массовый расход

получаем
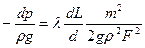
или
 (6.37)
(6.37)
Для изотермического течения газа по закону Бой л я
где  и
и  — давление и плотность газа в начале трубопровода.
— давление и плотность газа в начале трубопровода.
Подставим полученное значение 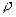 в уравнение (6.37) и проинтегрируем это уравнение в пределах от
в уравнение (6.37) и проинтегрируем это уравнение в пределах от  до
до  до где
до где  — давление в конце трубопровода длиной L,
— давление в конце трубопровода длиной L,
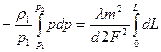 .
.
Отсюда получаем формулы, являющиеся основными формулами для расчета газопроводов при изотермическом течении газа: для определения падения давления в газопроводе
 ;
;  (6.38)
(6.38)
для определения массового расхода газа
m = F 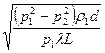 (6.39)
(6.39)
Коэффициент сопротивления % в этих формулах определяется по обычным формулам гидравлики вида 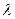 — f (Re,
— f (Re, 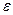 ), подробно рассмотренным ранее (см. § 46); при практических расчетах магистральных газопроводов часто применяют также и специальные «газопроводные» формулы, полученные в результате обработки опытных данных по перекачке газа. Наиболее широко используются (справедливые для всех зон турбулентного режима) универсальные формулы Кольбрука и Уайта (4.48) и Альтшуля (4.51) и формула ВНИИгаза (для квадратичной области)
), подробно рассмотренным ранее (см. § 46); при практических расчетах магистральных газопроводов часто применяют также и специальные «газопроводные» формулы, полученные в результате обработки опытных данных по перекачке газа. Наиболее широко используются (справедливые для всех зон турбулентного режима) универсальные формулы Кольбрука и Уайта (4.48) и Альтшуля (4.51) и формула ВНИИгаза (для квадратичной области)
 . (6.40)
. (6.40)
где d — диаметр трубопровода в см.
При выполнении инженерных расчетов формулам (6.38) и (6.39) часто придают следующий весьма удобный для практического использования вид:
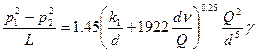 (6.41)
(6.41)
здесь р1 и p2 — абсолютное давление в начале и конце трубопровода в ата; L — длина трубопровода в км; d — диаметр трубопровода в см; k1 — эквивалентная шероховатость в см;  — удельный вес газа в кгс/м3; Q — расход газа в м3/ч;
— удельный вес газа в кгс/м3; Q — расход газа в м3/ч;  — кинематическая вязкость газа, м2/с;
— кинематическая вязкость газа, м2/с;  , Q и
, Q и  приведены к стандартным условиям: t = 0° С, р = 760 мм рт. ст.
приведены к стандартным условиям: t = 0° С, р = 760 мм рт. ст.
Отметим также, что в последнее время все большее развитие получает трубопроводный транспорт сжиженных газов, используемых как ценное сырье во многих химических производствах и дешевое топливо в быту.
Сжиженные газы представляют собой углеводороды, которые в чистом виде либо в виде смесей сравнительно небольшим повышением давления при температурах окружающей среды могут быть переведены из газообразного состояния в жидкое.
Основное требование, предъявляемое к трубопроводам, предназначенным для перекачки сжиженных газов, сводится к тому, чтобы ни в одном сечении трубопровода давление не снижалось ниже давления насыщения сжиженных газов (т. е. упругости их паров) при температуре перекачки. Если же давление упадет ниже этого значения, то, как уже указывалось ранее (см., например, § 31, стр. 98), жидкость закипит, в трубопроводе образуются паровые пробки и его пропускная способность резко уменьшится.
Поэтому при гидравлическом расчете подобных трубопроводов в целях обеспечения надежности их работы обычно принимают минимальное давление в трубопроводе значительно большим (на 10—12 кгс/см2), чем давление насыщения,
pmin =py +(10-12) (6.42)
В остальном же расчет ничем не отличается" от расчета обычных трубопроводов для капельных жидкостей.
ГЛАВА СЕДЬМАЯ БЕЗНАПОРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ
§ 77. РАВНОМЕРНОЕ ДВИЖЕНИЕ В ОТКРЫТЫХ КАНАЛАХ
Напомним, что при равномерном движении жидкости средние скорости во всех поперечных сечениях потока равны между собой. Поэтому равномерное движение жидкости в открытых каналах возможно только в том случае, когда форма и размеры поперечного сечения и уклон дна канала (а также и шероховатость стенок) остаются постоянными на всем его протяжении.
Очевидно, что при этом кривая свободной поверхности жидкости в канале будет параллельна линии дна канала и, следовательно,
уклон этой поверхности in будет равен уклону дна iД.
Равномерное движение обычно имеет место, например, в каналах гидростанций, ирригационных и осушительных каналах, трубопроводах, работающих неполным сечением (канализационные трубы, самотечные водоводы), и других потоках со свободной поверхностью. Рассмотрим сначала движение в открытых каналах.
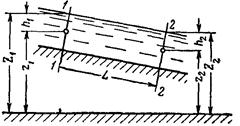
Рис. 181.
Составим уравнение Бернулли для сечений 1 – 1 и 2 – 2 открытого потока (рис. 181)при равномерном движении. В общем виде это уравнение (см. § 27) имеет вид
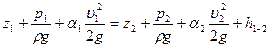 (7.1)
(7.1)
Здесь z1 и z2— расстояния до центров тяжести (вертикальные ординаты) сечений 1—1 и 2—2 от некоторой произвольной плоскости сравнения; рг и р2 — давления в центрах тяжести названных сечений и h1- 2 — потеря напора на длине L участка потока между ними.
Так как в рассматриваемом случае движение равномерное, то

Учтем далее, что р1 = ратм –рgh1 и рг = раты + Pgh2, где h1и h2 — глубины погружения центров тяжести сечений 1—1 и 2—2 под поверхностью жидкости. Поэтому уравнение (7.1) можно, переписать также следующим образом:
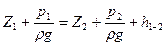
ИЛИ
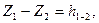 (7.2)
(7.2)
где Z1 и Z2 — расстояния от плоскости сравнения до свободной поверхности жидкости соответственно в сечениях /—/ и 2—2. Представляя потери напора в виде

вместо уравнения (7.2) получаем
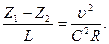

Отсюда
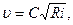 (7.3)
(7.3)
где 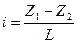 — уклон свободной поверхности, равный при равномерном движении уклону дна потока.
— уклон свободной поверхности, равный при равномерном движении уклону дна потока.
Полученная формула (7.3) есть формула Шези, уже рассматривавшаяся ранее (см. § 44); ей часто придают другой вид, обозначая произведение С 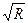 через W (так называемая приведенная скорость, или модуль скорости). Тогда
через W (так называемая приведенная скорость, или модуль скорости). Тогда
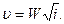 (7.4)
(7.4)
Расход жидкости в канале определяется по обычному уравнению расхода
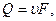
или
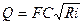 (7.5)
(7.5)
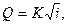 (7.6)
(7.6)
где
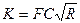 (7.7)
(7.7)
носит название пропускной способности, или модуля расхода. Приведенная скорость W и пропускная способность К для данного канала могут быть вычислены предварительно по известным размерам, форме сечения и шероховатости стенок канала, что значительно облегчает решение различных практических задач (при этом следует иметь в виду, что, так как гидравлический уклон i — число безразмерное, W и К имеют соответственно те же размерности, что v и Q, т. е. измеряются в м/с и м3/с).
При расчетах открытых каналов для определения коэффициента С (изменяющегося, как указывалось ранее, в зависимости от размеров и формы сечения канала и шероховатости его стенок) часто применяются уже рассмотренные выше (см. § 46) формула Маннинга
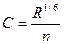 (7.8)
(7.8)
и формула Н. Н. Павловского
 (7.9)
(7.9)
а также формула И. И. Агроскина
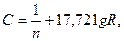 (7.10)
(7.10)
где п — коэффициент шероховатости, имеющий те же значения, что и в формуле Маннинга (см. табл. 20)
Следует иметь в виду, что приведенные формулы (7.8)—(7.10) применимы лишь для квадратичной области турбулентного режима, что практически обычно имеет место при движении в каналах воды.
В случае безнапорного движения в доквадратичной области турбулентного режима с известным приближением можно пользоваться соотношением

определяя коэффициент 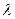 по соответствующим этой области формулам, после замены в них rили d гидравлическим радиусом сечения.
по соответствующим этой области формулам, после замены в них rили d гидравлическим радиусом сечения.
Более общий характер имеет обобщенная формула А. Д. Альтшуля
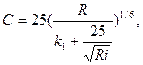 (7.11)
(7.11)
действительная для всей области турбулентного режима.
При больших уклонах и значительных шероховатостях эта формула упрощается и приводится к виду
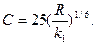 (7.12)
(7.12)
Для расчетов безнапорного движения в области ламинарного режима применяются специальные формулы (см. далее § 82).
1 При пользовании этой формулой величины R (гидравлический радиус) и kx (эквивалентная шероховатость) следует выражать в мм,
Дата добавления: 2015-04-18; просмотров: 2131; Мы поможем в написании вашей работы!; Нарушение авторских прав |