ГИДРАВЛИЧЕСКИ НАИВЫГОДНЕЙШЕЕ СЕЧЕНИЕ КАНАЛОВ

Из формулы Шези следует, что при прочих равных условиях скорость возрастает с увеличением гидравлического радиуса. Поэтому при одном и том же значении уклона канал с заданной площадью живого сечения F будет пропускать тем больший рас­ход, чем большим будет гидравлический радиус сечения. Для про­пуска наибольшего возможного при сечении F расхода форма сечения должна быть взята, следовательно, такой, при которой смоченный периметр А окажется наименьшим (поскольку R =F/A).

Из геометрии известно, что при одной и той же площади мень­шими периметрами обладают правильные многоугольники, при­чем их периметр будет тем меньше, чем больше число сторон.

Поэтому наименьшим периметром (из всех возможных) обладает круг и гидравлически наивыгоднейшим сечением для открытых каналов было бы сечение, имеющее форму полукруга. Далее идут различные сечения в форме половин правильных многоуголь­ников, например половина шестиугольника, т. е. равнобочная трапеция с углом наклона боковых сторон а = 60°. Из прямо­угольных профилей наивыгоднейшим является сечение в виде половины квадрата.

Для всех этих сечений, как нетрудно установить, гидравличе­ский радиус равен половине наибольшей глубины наполнения

что для полукруглого сечения соответствует половине радиуса круга

На практике широкое распространение получили каналы тра­пецеидального сечения; полукруглые же или многогранные се­чения применяются значительно реже из-за трудности их выпол­нения и значительной стоимости. Наиболее часто применяются каналы, открытые непосредственно в земле. В этих случаях, однако, трапецеидальные сечения редко получают форму наивыгод­нейшего профиля в виде половины правильного шестиугольника с углом а = 60°, так как при этом требуется искусственное креп­ление (обделка) боковых стенок канала. Обычно этот угол выби­рается в соответствии с углом естественного откоса грунта, и, таким образом, задача сводится к определению (при заданных площади сечения и угле откоса) соотношения между шириной и глубиной, при котором периметр будет наименьшим.

Углы откоса а (и соответствующие им значения откосов т = = ctg 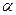) стенок канала для различных грунтов ориентировочно могут быть взяты из табл. 50.

Таблица 50 Значения углов откоса для различных грунтов

При заданной площади сечения F и угле откоса а для опреде­ления наивыгоднейших размеров сечения служат выражения:

(7.15)

из которого определяется глубина наполнения h, и

(7.16)

из которого по известному h может быть определено значение ши­рины bпо дну.

Эти выражения могут быть получены следующим образом. Из рис. 184 имеем

b₁=b+2hm

и

где

т — ctg .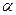

При этом для площади живого сечения получаем

Тогда смоченный периметр

A = b + 2a = b + 2h .

Подставляя сюда вместо b его значение из предыдущего выражения

находим

Как указывалось, для гидравлически наивыгоднейшего сечения при задан­ной постоянной площади сечения F смоченный периметр А должен быть наименьшим. Для определения минимального значения А возьмем производную и приравняем ее нулю

откуда

Заменив здесь f через bh + h² m, получим выражение (7.16). Нетрудно показать, что гидравлический радиус такого наивыгоднейшего сечения также равен половине его наибольшей глубины. На самом деле,

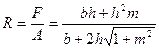
или, что то же самое,

Подставляя сюда вместо отношения — его значение из выражения (7.16),

получаем

и, следовательно,

§ 80. ДОПУСТИМЫЕ СКОРОСТИ

При больших скоростях движения жидкости в открытых ка­налах появляется опасность размыва стенок и дна канала. По­этому скорость приходится ограничивать до определенных пре­дельных значений, устанавливаемых в каждом отдельном случае в зависимости от рода грунта или способа укрепления русла, т. е. от материала стенок и дна канала. В табл. 51 приведены примерные значения предельных скоростей для различных грунтов при R = 14-3 м.

Таблица 51

Значения предельных скоростей для различных грунтов

Однако при очень малых скоростях взвешенные частицы (на­носы), влекомые потоком (муть, мелкий песок и т. д.), могут выпадать и откладываться на дне канала. Для предотвращения образования осадков на дне канала или, как говорят, заиления канала оказывается необходимым ограничивать также и наимень­шую среднюю скорость. Так, средняя скорость для воды, несущей муть, должна быть не менее 0,25 м/с, а для воды с мелким песком — не менее 0,5 м/с.

Наименьшая допустимая скорость для каналов значительной ширины определяется по эмпирической формуле

v = 0,55h⁰'⁶⁴, (7.17)

которая может быть представлена также и в более общем виде:

v =ah^0.64 . (7.18)

В этой формуле h — глубина наполнения канала, а — неко­торый коэффициент, значение которого выбирают в зависимости от состава наносов (табл. 52).

Таблица 52 Значения коэффициента а в формуле (7.18)

Для определения предельного уклона, при котором может начаться заиление канала, применяется формула

, (7.19)

пригодная для каналов гидравлически наивыгоднейшего сечения; здесь п — коэффициент шероховатости по Маннингу.

Необходимо учесть, что ввиду большой сложности указанных явлений приведенные здесь данные следует рассматривать как весьма приближенные, пригодные лишь для ориентировочных прикидочных) расчетов.