ВОДОСЛИВЫ

Водосливами называются искусственные преграды в потоке" со свободной поверхностью, поверх которых происходит перелив жидкости.

Водосливы широко применяются в гидротехническом и дорож­ном строительстве (водосливные плотины, водосбросы, пороги водобойных колодцев и т. п. ); они также используются в качестве измерителей расхода жидкости — главным образом в гидравли-

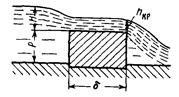
Рис. 189. Рис. 190.

ческих лабораториях, а также при гидрогеологических и гидро­метрических изысканиях в полевой обстановке; известное при­менение имеют водосливы и в нефтяной промышленности.

Водосливы классифицируются по ряду признаков.

Так, в зависимости от формы сливного порога, называемого гребнем водослива, различают следующие основные типы водо­сливов:

Рис. 191. Рис. 192.

1) водослив с тонкой стенкой или острой кромкой (рис. 189);

2) водослив с широким порогом (рис. 190), на таком пороге устанавливается почти параллельноструйное течение жидкости;

3) водослив практического профиля (рис 191), имеющий кри­волинейные очертания, соответствующие нижней поверхности струи жидкости в случае перелива через острый порог.

Области потока перед водосливом и после него называются соответственно верхним и нижним бьефами.

По типу сопряжения струи с нижним бьефом водосливы раз­деляются на незатопленные (см. рис. 189), когда уровень потока в нижнем бьефе непосредственно за водосливом не превышает гребня порога водослива, и затопленные (рис 192), когда этот уровень выше, чем гребень порога и его положение в нижнем бьефе существенным образом влияет на величину расхода, про­пускаемого через водослив.

В зависимости от расположения порога водослива в плане водослив может быть прямым (рис. 193, а), косым (рис. 193, б), ломаным (рис. 193, в) или криволинейным (рис. 193, г).

Если длина гребня водослива меньше ширины преграждаемого потока, то в зависимости от формы выреза в преграждающей

Рис. 193.

стенке водослив может быть прямоугольным (рис. 194, а), треуголь­ным (рис. 194, б), трапецеидальным (рис. 194, в), параболическим (рис. 194, г). Наконец, в зависимости от соотношения между дли­ной водослива и шириной потока перед ним различают водосливы без бокового сжатия и со сжатием. Боковое сжатие отсутствует в том случае, если длина гребня водослива совпадает с шириной

потока, что имеет место, например, при лабораторных водосливах, устанавливаемых в лотках прямоугольного

Рис. 194. Рис. 195.

сечения в качестве измерителей расхода и иногда в искус­ственных каналах. В прочих случаях всегда имеет место боко­вое сжатие, обусловленное стенками, ограничивающими гребень водослива (рис. 195), или наличием промежуточных бычков.

Основной задачей при гидравлическом расчете водослива является определение расхода жидкости, протекающей через него.

Исследуем под этим углом зрения истечение жидкости через водослив с тонкой стенкой; сначала рассмотрим прямоугольный водослив без бокового сжатия (рис. 196).

По мере приближения к водосливу уровень свободной по­верхности перед ним постепенно снижается и принимает форму кривой спада. Снижение уровня перестает быть практически заметным на расстоянии от водослива (отсчитываемом против те­чения), равном примерно 3Н, где Н — погружение гребня водослива под неискаженным уровнем в верхнем бьефе; эта вели­чина называется напором на водосливе.

Для определения расхода жидкости через такой водослив служит общая формула, применимая, как мы это увидим в даль­нейшем, для водосливов всех типов,

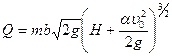(7.26)

Рис. 196.

где т — коэффициент расхода водослива; b — ширина порога водослива; Н — напор над порогом водослива; v₀ — скорость подхода жидкости к гребню водослива; 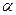— коэффициент неравно­мерности распределения скоростей. В тех случаях, когда ширина и глубина подводящего канала перед водосливом достаточно велики, ско­ростью подхода можно пренебречь и формула (7.26) примет вид

(7.27)

Приведенные формулы могут быть получены, если рассматривать перете­кание жидкости через водослив как истечение из большого прямоугольного отверстия в тонкой стенке шириной b и высотой Н с отсутствующим верхним ребром. Подобная задача уже была решена нами (см. § 58). Там же для определения расхода была выведена формула (5.19).

Если при выводе этой формулы принять Н₁ = О и заменить H₂ через Н, что соответствует случаю водослива, то пределы ин­тегрирования при учете скорости подхода будут равны: верхний,

предел , нижний предел , и формула (5.19) примет вид

Пренебрегая здесь вторым слагаемым в квадратных скобках ввиду его относительной малости, обозначая 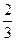через m и вводя коэффициент а, учитывающий неравномерность распреде­ления скоростей, приходим к формуле (7.26).

Если же скорость подхода не учитывать (v₀ = 0), получим формулу (7.27).

Величина коэффициента расхода m в формуле (7.26) опреде­ляется опытным путем и для рассматриваемого водослива зависит, как показывает опыт, от напора Н и высоты водосливного по­рога Р. Для других водосливов коэффициент расхода зависит также от формы порога, бокового сжатия и характера сопряжения струи с нижним бьефом. Поэтому, по Н. Н. Павловскому, общее выражение для коэффициента расхода будет

(7.28)

где т_r — так называемый приведенный коэффициент расхода (т. е. коэффициент расхода в случае = 1); — коэф­фициент формы, зависящий от формы гребня, водослива; — коэффициент напора, зависящий от напора над порогом водо­слива; — коэффициент затопления, зависящий от характера сопряжения струи с нижним бьефом; — коэффициент, завися­щий от сжатия струи.

Ниже приводятся эмпирические формулы для коэффициента расхода водослива для некоторых основных случаев.

Для незатопленного прямоугольного водослива с тонкой стенкой без бокового сжатия (см. рис. 189) этот коэффициент

(7.29)

При ориентировочных расчетах, как среднее значение, можно принимать т = 0,41 -0,42.

Для этого же водослива с боковым сжатием, т. е. когда ши­рина порога водослива b меньше ширины канала В (при ),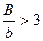

(7.30)

Если водослив затопленный, то коэффициент т умножается на коэффициент затопления, определяемый формулой

, (7.31)

где z — перепад между уровнями в верхнем и нижнем бьефах, a h = H — z (см. рис. 192).

Следует также иметь в виду, что для затопленного водослива «с тонкой стенкой должны выполняться условия

h>0; . (7.32)

Если же при h > 0 , > 0,7, водослив будет работать как незатопленный.

Для измерения расхода жидкости часто используются трапецеидальный и треугольный водосливы с тонкой стенкой.

Расход жидкости в трапецеидальном водосливе (см. рис. 194, в) -определяется по формуле

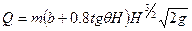, (7.33)

где т — коэффициент расхода, определяемый опытным путем; b — ширина водослива по низу; — угол наклона боковой стенки. При значении tg (уклон боковой стенки) = 0,25 трапеце­идальный водослив обладает свойством постоянства коэффициента расхода (т = 0,42) при изменении напора и в таком виде обычно и применяется для измерения расхода. В этом случае

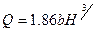(7.34)

Для водослива треугольной формы (см. рис. 194, б)

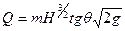(7.35)

Наибольшее применение имеет треугольный водослив с выре­зом в форме прямоугольного треугольника (2 = 90°), обычно используемый для измерения сравнительно небольших расходов жидкости. Для такого водослива

. (7.36)

ГЛАВА ВОСЬМАЯ

ДВИЖЕНИЕ ЖИДКОСТИ В ПОРИСТОЙ СРЕДЕ

§ 84. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

В ряде областей техники приходится иметь дело с движением различных природных жидкостей в естественном грунте. Приме­рами этого является движение нефти в нефтеносных пластах к неф­тяным скважинам, движение грунтовых вод в водоносных пла­стах, используемых для целей водоснабжения, движение воды под гидротехническими сооружениями (например, плотинами) и т. д. Во всех этих случаях жидкость просачивается через грунт, т. е. движется внутри пор грунта, перемещаясь по мельчайшим каналам, образующимся между его частицами вследствие их не­полного прилегания друг к другу. Такое движение жидкости называют фильтрацией.

Если проницаемый пласт залегает на непроницаемом основании и не перекрывается сверху непроницаемым слоем, фильтрация происходит с образованием свободной поверхности, давление на которой равно атмосферному (рис. 197). Движение в этом случае называется безнапорным. Если же фильтрация происходит в пла­сте, заключенном между двумя непроницаемыми пластами без образования свободной поверхности (рис. 198), движение назы­вают напорным.

Основной задачей при практических расчетах в области филь­трации является определение расхода, т. е. количества фильтру­ющейся жидкости и скорости фильтрации, под которой понимают расход жидкости через единицу площади поперечного сечения всего фильтрующего слоя (включая как сам грунт, так и поры между его частицами). Следует иметь в виду, что скорость фильтрации, конечно, отлична от физической скорости движения частиц жидко­сти по поровым каналам.

Скорость фильтрации определяется гидравлическим уклоном и физическими свойствами фильтрующейся жидкости и грунта. Физические свойства жидкости определяются ее вязкостью и удельным весом. Фильтрационные же свойства грунта зависят от размеров и формы отдельных составляющих его частиц и харак­теризуются пористостью и просветом грунта.

Пористостью, или, иначе, коэффициентом пористости т, называется отношение объема пор, т. е. пустот между отдельными частицами грунта, ко всему объему грунта

(8.1)

где V₁ – полным объем грунта; V₂ — суммарным объем твердых частиц..

Под просветом, m.'iii коэффициентом просветности, понимают отношение площади сечения пор к площади всего сечения грунта.

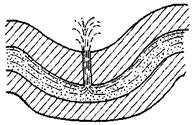
Рис.197. Рис. 198.

Физически просвет характеризует собой живое сечение потока фильтрующейся жидкости и определяется выражением

, (8,2)

где 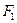- общая площадь сечения грунта; F₂ — часть этой пло­щади, приходящаяся па долю грунта.

Пористость природных естественных грунтов изменяется в весьма широких пределах. Так, нефтеносные рыхлые (несцемен­тированные) пески имеют пористость т = 0,30-0,33; для песков же с гли­нистыми частицами и отложениями солей т — 0,18-0,24 для известняков т — 0,025-0,12. Величина порис­тости естественного грунта в каждом отдельном случае может быть уста­новлена опытным путем.

Естественные грунты состоят из частиц неправильной формы различных размеров; это делает

Рис. 199.

теоретическое исследование фильтрации чрезвычайно

сложным, и для упрощения обычно

исходят из условной модели — так называемого фиктивного грунта, состоящего из частиц правильной шарообразной формы одинакового диаметра, гидравлически эквивалентного естествен­ному грунту. Значения пористости и просвета для фиктивного грунта могут быть подсчитаны теоретически.

Для перехода от естественного грунта к фиктивному вводится понятие о так называемом эффективном или действующем диаметре, определяемом на основе механического анализа грунта, заклю­чающегося в просеивании грунта через калиброванные сита с отвер­стиями различной величины. По данным анализа строятся грану­лометрическая (весовая) кривая (рис. 199), для чего по оси абсцисс откладывают диаметры d зерен грунта (в мм), а по оси Ординат — суммарный вес всех фракций, начиная от нуля до данного диа­метра, в процентах от общего веса всей пробы. За эффективный диаметр d_eпринимается, например, такой диаметр зерен, при котором суммарное процентное содержание фракций более мел­кого размера составляет 10% от общего веса.

§ 85. ОСНОВНЫЕ ЗАКОНЫ ФИЛЬТРАЦИИ

Первые исследования движения жидкости в пористых телах были проведены в середине XIX в. французским гидравликом Дарси.

В своих опытах Дарси применял прибор (рис. 200), состоящий из вертикального цилиндрического сосуда, заполненного слоем

песка, через который при постоянной разности напоров пропускалась вода. Определяя при помощи пьезометров давле­ния в различных по высоте сечениях фильт­рующего слоя, изменяя толщину этого слоя и состав песка и измеряя расход фильт­руемой воды, Дарси установил основной закон фильтрации, которому подчиняются различные несжимаемые жидкости (вода, нефть) при своем движении через грунт. Этот закон носит название закона Дарси и имеет следующее математическое вы­ражение:

(8.3)

Рис. 200. где Q — расход жидкости при фильтрации; k — коэффициент фильтрации, ха­рактеризующий одновременно как фильтрационные свойства пористой среды — грунта, так и физические свойства фильтрую­щейся жидкости; F — площадь фильтрации, под которой (на­помним) понимают полное сечение всего фильтрующего слоя, включая как caw грунт, так и поры между отдельными его частицами (для рассматриваемого случая F есть площадь попереч­ного сечения сосуда); h — потеря напора:

и определяемая по разности показаний пьезометров (здесь 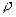— плотность жидкости); L — толщина слоя грунта в направлении фильтрации.

Уравнение (8.3) можно представить также в более простой форме

, (8.4)

где

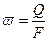
— средняя в сечении фильтрующего слоя скорость фильтрации, а

— гидравлический уклон, представляющий собой падение напора на единицу длины.

Из этой формулы следует, что коэффициент фильтрации имеет размерность

т. е. размерность скорости (так как гидравлический уклон есть величина безразмерная). Обычно он измеряется в сантиметрах в секунду (см/с). Отсюда видно также, что при i = 1 k = , т. е. физически коэффициент фильтрации представляет собой скорость фильтрации при единичном уклоне.

Дарси проводил свои опыты с водой. В дальнейшем при иссле­довании фильтрации других жидкостей было установлено, что скорость фильтрации обратно пропорциональна вязкости. В связи с этим вязкость жидкости была выделена в отдельный параметр.

В то же время скорость фильтрации стали определять не через перепад напора h, а исходя из разности давлений 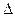р, соответству­ющей этому перепаду ( 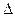р = pgh). Таким образом,

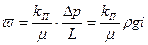(8.5)

где k_n — коэффициент проницаемости, характеризующий филь­трационные свойства самого грунта; — абсолютная вязкость жидкости.

Коэффициент проницаемости связан с коэффициентом фильтра­ции соотношением

, (8.6)

легко получаемым из сопоставления формул (8.4) и (8.5).

Размерность коэффициента проницаемости

т. е. размерность площади.

В международной системе единиц коэффициент проницаемости измеряется в квадратных метрах; в физической системе единиц — в квадратных сантиметрах. За практическую же единицу коэф­фициента проницаемости принимают проницаемость грунта, ко­торый при площади фильтрации F — 1 см², толщине слоя филь­трации L — 1 см, абсолютной вязкости фильтрующейся жидкости = 0,01 г/см*с (сП — сантипауз) и потере давления 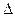р (соот­ветствующей потере напора К) =1 кгс/см² (ат) пропускает расход жидкости Q = 1 см³/с. Такая единица проницаемости называется даре и (обозначается Д); единица, равная 0,001 дарси, носит название миллидарси (мД),

Закон Дарси часто называют законом ламинарной фильтрации, так как согласно этому закону расход и скорость фильтрации ли­нейно зависят от потери напора, что является первым признаком ламинарного режима и уже отмечалось ранее при рассмотрении движения жидкости в трубопроводах. В большинстве случаев движение жидкости в пористых телах действительно происходит с весьма малыми скоростями, а сечения отдельных пор грунта также весьма малы, что делает возможным уподобить фильтрацию ламинарному движению в тонких неправильной формы капилляр­ных трубках. Поэтому закон Дарси, хорошо согласующийся с действительностью, является основным законом фильтрации и обычно используется при решении различного рода практиче­ских задач в этой области.

В отдельных случаях, когда движение жидкости в грунте характеризуется значительными скоростями, что может иметь место в крупнотрещиноватых и крупнопористых породах (напри­мер, в галечниках и скальных породах), наблюдается переход к турбулентному режиму. Закон Дарси здесь нарушается, и формулы (8.3) и (8.4) неприменимы.

Закон Дарси неприменим также и при фильтрации в весьма мелкозернистых глинистых грунтах с очень малыми скоростями, когда, начинают заметно сказываться капиллярные силы поверх­ностного натяжения. Эти случаи не имеют, однако, особенного практического значения, так как даже при весьма малых разме­рах частиц грунта, диаметром всего лишь около 0,05 мм, и неболь­ших скоростях фильтрации закон Дарси все еще оказывается справедливым.

Граница перехода от ламинарного режима к турбулентному устанавливается по критическому значению числа Рейнольдса, для определения которого при фильтрации предложен ряд эмпи­рических формул. Так, по Н. Н. Павловскому,

(8,7)

по В. Н. Щелкачеву:

(8.8)

где — кинематическая вязкость жидкости, а остальные обозна­чения те же, что и ранее.

Критическое значение числа Рейнольдса при его определении по формуле Павловского лежит в интервале

а по формуле Щелкачева —

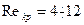
Для определения скорости фильтрации при турбулентном ре­жиме применяются следующие формулы: формула Краснопольского (в форме, приданной ей Щелкачевым)

(8,9)

где 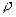— плотность жидкости, и формула Смрекера

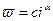(8 10)

где с — коэффициент пропорциональности, определяемый опыт­ным путем; 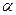— показатель степени, изменяющийся в зависимости от вида грунта в пределах от 1/3 до 1.