БЕЗНАПОРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ПОРИСТОЙ СРЕДЕ

В качестве примера безнапорного движения жидкости в пори­стой среде рассмотрим откачку воды из колодца или скважины, заложенной в водоносном пласте с горизонтальным непроницае­мым подстилающим слоем. До начала откачки грунтовые воды в пласте находятся в покое и поверхность их горизонтальна. Если откачивать воду из колодца, в водоносном слое начнется движение грунтовых вод к колодцу. При этом уровень воды в ко­лодце понизится. Одновременно произойдет понижение уровня грунтовых вод в пласте; это понижение будет наибольшим у сте­нок колодца, постепенно убывая по мере отдаления от него

Рис. 201.1 Рис. 202.

(рис. 201). Чем интенсивнее будет производиться откачка, тем ниже будет располагаться уровень воды в колодце и тем больше будет его дебит (расход).

Уровень стояния воды в колодце до начала откачки H_ст, оди­наковый с уровнем во всем водоносном пласте, обычно называют статическим. Уровень H_д, устанавливающийся в колодце в про­цессе откачки, носит название динамического, а сечение открытой поверхности уровня воды в пласте вертикальной плоскостью, проходящей через ось колодца, называется кривой депрессии, или кривой падения уровня (схематически показана пунктиром на рис. 214).

В действительности кривая депрессии выклинивается на стенках колодца несколько выше поверхности воды в нем, образуя так называемый «промежуток высачивания» (рис. 202). На этом промежутке (ВС) вода будет сочиться в атмосферу истекать в колодец вдоль его стенок. Действительная кривая депрессии изобра­жается кривой АВСС'В'А'.

При откачке из одиночного колодца (скважины) снижение уровня, вызываемое откачкой, на некотором расстоянии от оси колодца практически перестает быть заметным; это расстояние называется радиусом дренирования, или радиусом влияния ко­лодца (скважины). При предварительных расчетах его можно принимать равным для песчаных грунтов от 350 до 500 м, для крупнозернистых грунтов — 700 м.

Предполагая этот радиус R известным, зная толщину (мощ­ность) водоносного слоя и задаваясь динамическим уровнем в колодце, можно определить расход воды в колодце и установить приближенную форму депрессионной кривой.

Для этого рассмотрим движение воды через некоторое цилиндрическое се­чение водоносного слоя на расстоянии х от оси колодца. Если глубина воды в этом сечении h, площадь сечения будет

F = 2 xh.

При этом расход фильтрации

Q = F = 2 xh,

где — скорость фильтрации, определяемая, как обычно, по формуле Дарси (8.4)

= ki.

Подставляя это значение скорости в выражение для расхода, получаем

Q = k2 xhi.

Гидравлический уклон в этом выражении можно заменить через отношение бесконечно малой потери напора, т. е. падения уровня dh, к бесконечно малому пути в радиальном направлении dx

Тогда

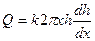
Разделив переменные

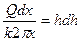
и проинтегрировав это уравнение в пределах для х от г₀ до R (где г₀ — радиус колодца) и соответственно для h от Н_д до Н_ст, т. е. пренебрегая участком высачивания,

получим выражение

(8,15)

известное под названием формулы Дюпюи.

Расход, т. е. искомый дебит колодца, определяется выраже­нием

(8.16)

Для определения формы кривой депрессии необходимо, задаваясь различными значениями х (вместо R), определить из уравнения (8.15) соответствующие им значения h (вместо Н_д) и по точкам построить кривую, которая представляет собой параболу в коор­динатах , h.

Опытными проверками установлено, что расход, определяемый по формуле Дюпюи, совпадает с действительным расходом, не­смотря на неучет промежутка высачивания; положение же кривой депрессии при этом, естественно, определяется лишь приближенно.