ВЯЗКО-ПЛАСТИЧНЫЕ ЖИДКОСТИ И ИХ СВОЙСТВА

Вязко-пластичные жидкости представляют собой нечто среднее между жидкими и твердыми телами и известным образом совме­щают в себе свойства как вязкой ньютоновской жидкости, так и твердого пластичного тела. К их числу, например, относятся различного рода суспензии и коллоидальные растворы, состоящие из двух фаз — твердой и жидкой, глинистые и цементные растворы, парафинистые нефти, битумные изоляционные материалы.

Свойства ньютоновской жидкости были рассмотрены выше. Остановимся на понятии идеального пластичного тела.

Рис. 210.

В таком пластичном теле при малых действующих нагрузках, а следовательно, и малых напряжениях возникают упругие де­формации; после снятия нагрузки эти деформации исчезают и тело восстанавливает свою первоначальную форму. Когда на­пряжение достигает некоторого предельного значения т₀, назы­ваемого пределом текучести, или начальным напряжением сдвига, пластичное тело начинает течь. В дальнейшем это напряжение все время сохраняется постоянным при любых значениях относи­тельной скорости сдвига.

Кривая течения подобного идеального пластичного тела пред­ставляет прямую линию, параллельную оси ординат и отстоящую от нее на расстоянии, равном т₀ (кривая // на рис. 210, б); ее уравнение

(9.4)

Если теперь просуммировать абсциссы этой кривой и кривой / (рис. 210, а) течения ньютоновской жидкости, как это показано на том же рисунке (рис. 210, в), получим кривую ///, представ­ляющую собой кривую течения вязко-пластичной жидкости, те­чение которой, как и у идеального пластичного тела, начинается при напряжении, равном начальному напряжению сдвига 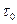, и продолжается далее при напряжениях, изменяющихся по линейному закону, так же, как и у обычных ньютоновских жидко­стей. Уравнение такой кривой получается комбинацией уравне­ний (4.1) и (9.4) и имеет следующий вид:

(9,5)

В честь американского ученого Бингама, установившего в 1916 г. эту зависимость и описавшего свойства подобной вязко-пластической жидкости, ее обычно называют бингамовской жидко­стью .

Реологические свойства бингамовской жидкости характери­зуются двумя основными параметрами:

начальным напряжением сдвига т₀ (на реограмме — отрезок оси абсцисс, отсекаемый кривой течения от начала координат);

бингамовской, или пластической, вязкостью, определяемой по углу а наклона кривой течения к той же оси

(9.6)

При гидравлических расчетах используется также установлен­ное ранее (стр. 287) понятие эффективной (кажущейся) вязкости, которая в этом случае определяется выражением

(9.7)

Механизм поведения бингамовских жидкостей можно объяс­нить образованием в покоящейся жидкости жесткой простран­ственной решетки (например, у парафинистых нефтей из кристал­лов парафина), заполненной жидкой фазой (нефтью). Жесткость этой решетки (структуры) такова, что она приводит к полной потере подвижности и достаточна для того, чтобы сопротивляться , любому напряжению, не превосходящему по величине т₀. Если напряжение превышает т₀, то структура разрушается и система ведет себя как обычная ньютоновская жидкость при напряжениях сдвига . Когда же напряжение сдвига становится меньше т₀, структура снова восстанавливается.

Естественно, что подобное представление о бингамовской жидкости является в известной степени условным и схематизиро­ванным. Однако оно оказывается весьма удобным для практиче­ских целей, так как многие реальные жидкости весьма близки к этой схеме — характеризуются теми же основными свойствами, что и бингамовская жидкость, и имеют однотипные с ней по своей форме кривые течения.

Для многих неньютоновских жидкостей начальное напряжение сдвига в значительной степени зависит от времени нахождения жидкости в покое; как правило, с течением времени консистенция этих жидкостей изменяется — они как бы застудневают и их

начальное напряжение сдвига увеличивается. Это свойство не­ньютоновских жидкостей называется тиксотропией, а подобные жидкости — тиксотропными.

Поэтому в общем случае (рис. 211, а) необходимо различать: статическое начальное напряжение сдвига , характеризующее напряжение в начальный момент движения, когда жидкость вы­водится из состояния покоя, и динамическое начальное напряже­ние сдвига т₀ , представляющее собой минимальное напряжение, необходимое для движения, если рассматривать жидкость как

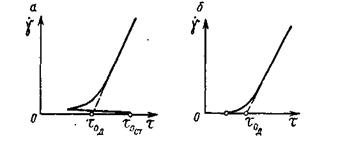
Рис. 211.

бингамовскую, т. е. если кривая течения будет полностью заме­нена прямой линией (показана пунктиром).

Следует отметить, что при обычных лабораторных измерениях, ввиду ограниченной чувствительности измерительных приборов, начальный участок кривой течения (вблизи ), соответству­ющий весьма малым значениям градиентов скорости , часто не удается получить и кривая течения представляется в виде, изображенном на рис. 211, б.

Статическое начальное напряжение сдвига необходимо для решения различных задач, в которых рассматриваются начальные (пусковые) стадии движения; примером подобной задачи может служит расчет процесса выталкивания насосами застывшей парафинистой нефти из остановленного трубопровода.

Во всех же остальных случаях при обычных гидравлических расчетах, связанных с движением неньютоновских жидкостей в различных гидравлических системах, используется динамиче­ское начальное напряжение сдвига.