ДВИЖЕНИЕ ВЯЗКО-ПЛАСТИЧНЫХ ЖИДКОСТЕЙ ПО ТРУБАМ

Движение неньютоновских жидкостей по трубам и лоткам характеризуется рядом особенностей по сравнению с движением обычных жидкостей. Как показывает опыт для начала движения неньютоновской жидкости необходимо создать некоторую определенную разность напоров, соответствующие, как уже указывалось ранее (см. § 40), равенству возникающего в жидкости касательного напряжения сдвига начальному напряжению сдвига 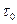. При этом вся масса жидкости отрывается от стенок трубы или лотка и движется первоначально как одно целое (т. е. как твердое тело) с одинаковыми скоростями для всех частиц.

Рассмотрим этот случай и определим разность напоров, необ­ходимую для начала движения неньютоновской (бингамовской) жидкости, заполняющей горизонтальный цилиндрический трубо­провод длиной l и диаметром d. Давление в концевых сечениях трубопровода обозначим через p₁ и p₂ плотность и удельный вес жидкости — через р и у и ее начальное напряжение сдвига — через .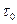

Так как в рассматриваемом случае силы трения будут возни­кать только у стенок трубы на боковой поверхности выделенного объема жидкости и равнодействующая этих сил

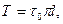
то уравнение равновесия, составленного для системы сил, дей­ствующих на этот объем, по аналогии с выводом общего выраже­ния для потерь напора при равномерном движении (см. § 36), будет иметь вид

Отсюда получим следующие выражения:

для разности давлений на концах трубопровода

(а)

для разности напоров в тех же сечениях

(b)

Таким образом, если

(с)

жидкость в трубопроводе будет двигаться, причем в зависимости от приложенной разности напоров Н₁—Н₂ здесь могут иметь место три, различных режима ее движения: структурный, ламинар­ный и турбулентный.

Выражение (с) является исходным при исследовании началь­ных стадий движения (например для расчета процесса выталки­вания застывшей высокопарафинистой нефти из остановленного трубопровода); при этом, как уже указывалось, под 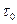следует понимать статическое начальное напряжение сдвига 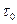; во всех же остальных случаях движения неньютоновских жидкостей по трубам .

Поясним не встречавшееся ранее определение структурного режима.

Вначале при соблюдении равенств (а) и (Ь) весь поток жидкости движется целиком как твердое тело с одинаковой скоростью по всему поперечному сечению. По мере увеличения разности на­поров 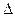Н возрастает и скорость движения жидкости и в ближай­ших к стенкам трубы частях потока развивается ламинарный режим, в центральной же его части (так называемое центральное ядро) жидкость по-прежнему продолжает двигаться как твердое тело.

Такой режим движения жидкости, характеризующийся нали­чием центрального ядра, называется структурным.

Радиус центрального ядра может быть найден путем рассу­ждений, аналогичных сделанным выше, и определяется выраже­нием

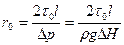(9,8)

При дальнейшем возрастании 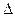Н область ламинарного режима будет расширяться, размеры же центрального ядра — соответственно уменьшаться. Повышая АН, можно достичь того, что структурный режим полностью перейдет в ламинарный (что соот­ветствует значению r₀ = 0).

В дальнейшем в трубопроводе начнет развиваться турбулент­ный режим, наиболее часто встречающийся в обычных условиях практики.

Следует отметить, однако, что в действительности турбулент­ность начинает зарождаться в потоке еще при наличии централь­ного ядра; поэтому полностью ламинарный режим обычно не имеет места и структурный режим переходит непосредственно в турбулентный.

Установим закон распределения скоростей в поперечном се­чении трубы при структурном режиме. Для этого будем исходить из общего уравнения (9.5) для касательного напряжения в ненью­тоновской (бингамовской) жидкости.

Для любого цилиндрического слоя жидкости радиусом у > г₀ касательное напряжение в соответствии с выражением (4.18) равно

Подставим это значение в уравнение (9.5) и представим его в виде

Умножив далее обе части этого уравнения на dy и проинтегрировав

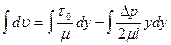
получим

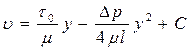
Постоянную интегрирования находим из условий у стенок трубы: при у = r, 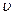=0; следовательно,

Таким образом, получаем следующую формулу для распреде­ления скоростей при структурном режиме:

(9.9)

Кривая скоростей, соответствующая этой формуле, представлена на рис. 212. Она состоит из двух частей: двух параболических ветвей у стенок в зоне ламинар­ного режима и прямолинейного участка в центральном ядре.

Для определения скорости дви­жения центрального ядра в формуле (9.9) необходимо

Рис. 212.

принять у = г₀; при этом получаем

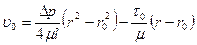(9.10)

В частном случае, когда ₀ = 0, формула (9.9) превращается ,в обычную формулу Стокса для ламинарного режима (ей соответ­ствует пунктирная кривая на рис. 212).

Расход жидкости при структурном режиме может быть опре­делен как сумма расходов в центральном ядре (Q_ц) и в ламинарной части потока (Q_л)

Q= Q_ц + Q_л

Таким образом, имеем

где v₀ и v — соответственно постоянная скорость в ядре и скорость в ламинарной части потока, определяемые формулами (9.10) и (9.9).

В результате интегрирования этого выражения после ряда преобразований и упрощений приходим к формуле, известной под названием формулы Букингама:

(9,11)

где 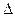р — приложенная разность давлений; 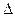р₀ — разность дав­лений, соответствующая началу движения жидкости, вычисляе­мая по формуле (а).

Практически при значительном перепаде давлений, что часто наблюдается в реальных условиях, последним членом в этом урав­нении вследствие его малости по сравнению с остальными сла­гаемыми оказывается возможным пренебречь, и формула (6.11) принимает более простой вид

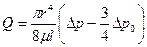(9.12)

Потери напора при движении некьютоновских (бингамовских) жидкостей можно определять по обычной формуле Дарси—Вейсбаха (4.45).

При этом в случае структурного и ламинарного режимов для коэффициента гидравлического сопротивления используют выра­жение

(9,13)

где Re * — так называемое обобщенное число (критерий) Рей­нольдса, учитывающее одновременно как вязкие, так и пластиче­ские свойства жидкости.

Обобщенное число Рейнольдса

(9,14)

здесь — обычное число Рейнольдса; Sen = 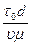- число Сен-Венана (характеристика пластических свойств жидко­сти); А — некоторый коэффициент, зависящий от структуры потока, определяемой радиусом его центрального ядра.

При практических расчетах, исходя из результатов экспери­ментальных исследований, часто полагают А = ¹/₆. Тогда выра­жение для обобщенного числа Рейнольдса принимает вид

(9.15)

Более общим является выражение для обобщенного числа Рей­нольдса, установленное Е. 3. Рабиновичем,

(9.16)

где а — так называемая структурная характеристика потока, которая зависит от отношения r₀/r = с и изменяется в пределах от а = 3 (при с — 0) до а = 6 (при с = 1); значения а находятся по специальной номограмме (рис. 213).

Рис. 213.

При турбулентном режиме для определения коэффициента применяют формулы типа

(9.17)

где коэффициент В и показатель степени п наиболее достоверно устанавливают по результатам обработки опытных данных. Так, по Б. С. Филатову, для неутяжеленного глинистого раствора В — = 0,1» п = 0,15; для утяжеленного глинистого раствора ( > > 1,8 гс/см²) В = 0,0025, п = —0,2; при этом формула (9.17) принимает соответственно вид:

(9.18)

И

. (9.19)

Коэффициент X (как при структурном и ламинарном, так и при турбулентном режимах) можно определять также и по обычным формулам гидравлики ньютоновских жидкостей (4.47) и (4.54), вводя в них вместо Re так называемое эффективное число Рейнольдса Re*_кр, определяемое по эффективной (кажущейся) вязкости (см. § 40).

В заключение отметим, что режим течения неньютоновских жидкостей определяется по критическому значению обобщенного числа Рейнольдса Re*_э. До сих пор, однако, этот вопрос не нашел своего окончательного решения. Отдельные исследователи считают, что в случае неньютоновских жидкостей число Re£_p имеет большее значение, чем для жидкостей ньютоновских; другие придерживаются противоположной точки зрения.

При практических расчетах часто поступают следующим обра­зом. По формуле

(9.20)

(обозначения прежние) находят так называемую критическую ско­рость и, сравнивая ее со средней скоростью потока и, устанавли­вают характер режима: при v < v_кp — режим структурный, при v > v_кp — режим турбулентный.