ГИДРАВЛИЧЕСКИЕ РАСЧЕТЫ ОТКРЫТЫХ КАНАЛОВ

При гидравлическом расчете открытых каналов встречаются задачи следующих основных типов:

1) определение расхода жидкости, пропускаемой данным ка­налом;

2) определение уклона дна, необходимого для пропуска задан­ного расхода жидкости в канале заданной формы сечения с извест­ной глубиной наполнения;

3) определение глубины наполнения или ширины канала для пропуска данного расхода жидкости при известном уклоне дна.

Рис. 182. Рис. 183.

При решении указанных задач будем исходить из формулы Шези (7.3)

Подставив в нее значение коэффициента С в его выражении, например по^Маннингу, получим

(7.13)

При этом для расхода будем иметь

(7.14)

Значения площади живого сечения F и гидравлического ра­диуса R в этой формуле зависят от глубины наполнения канала h и от формы его поперечного сечения, коэффициент же шерохова­тости является заданной величиной.

Если известны форма поперечного сечения канала и глубина его наполнения,, находят модуль расхода

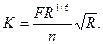
После этого по формуле (7.14) определяют расход для задан­ного уклона или уклон, необходимый для пропуска заданного расхода.

Если же известны расход и уклон канала [и требуется опре­делить глубину его наполнения, поступают следующим образом: задаются формой поперечного сечения канала и несколькими зна­чениями глубины его наполнения h. Далее вычисляют соответству­ющие этим наполнениям значения модуля расхода К и строят кривую для К в зависимости от h (рис. 182). Затем откладывают по оси абсцисс значение модуля К. (соответствующее заданному рас­ходу) и по кривой определяют искомую глу­бину наполнения h_p.

В том случае, когда известна глубина наполнения и необходимо найти ширину канала, поступают аналогично предыду­щему — строят график изменения модуля расхода К в зависимости от ширины b и находят по этому графику искомую ширину канала Ъ_р (рис. 183).

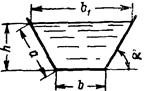
Рис.184.

Подобные задачи могут быть решены также и аналитически, если предвари­тельно выразить через глубину наполнения ft величины F и R. Так, в случае пря­моугольного сечения шириною В имеем

F=bh,

При трапецеидальном русле (рис. 184)

F = bh + h²m,

где т = ctg a.

Подставляя эти выражения для F и R в формулу (7.14), получаем уравнение с одним неизвестным h; практически определение глубины h по кривой (описанное выше) оказывается более простым.