Основное уравнение гидростатики

Уравнение равновесия жидкости может быть записано в дифференциальной форме (уравнение Л. Эйлера):

, (1)

где X, Y, Z- проекции массовых сил на оси координат, отнесенные к единице массы;

r - плотность жидкости, кг/м³.

Основное уравнение гидростатики имеет вид:

(2)

гдеZ₁, Z₂- расстояния от плоскости сравнения до рассматриваемых точек;

р₁, р₂ - гидростатические давления в этих точках;

g - ускорение силы тяжести, g = 9,8 м/с².

В соответствии с основным уравнением гидростатики абсолютное гидростатическое давление в точке определяется по формуле

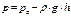, (3)

где р_о - давление на свободной поверхности или внешнее давление, Па;

h - глубина погружения точки под свободной поверхностью, м.

Произведение называется избыточным или весовым давлением.

Задачи

Задача 9. Определить избыточное давление воды в трубе по показаниям батарейного ртутного манометра. Отметки уровней ртути от оси трубы: z₁=1,75 м; z₂=3 м; z₃=1,5 м; z₄=2,5 м; (рис. 1).

Задача 10. Определить давление в резервуаре р₀ и высоту подъема уровня воды h₁ в трубке l, если показания ртутного манометра h₂=0,15 м и h₃=0,8 м (рис. 2).

Задача 11. Два горизонтальных цилиндрических трубопровода А и В содержат соответственно минеральное масло плотностью r_м=900 кг/м³ и воду плотностью r_в=1000 кг/м³. Высоты жидкостей, представленные на рис. 3, имеют следующие значения: h_м=0,2 м; h_рт=0,4 м; h_в=0,9м. Зная, что гидростатическое давление на оси в трубопроводе А равно 0,6∙10⁵ Па, определить давление на оси трубопровода В.

Задача 12. К всасывающей стороне цилиндра присоединен водяной вакуумметр с показанием h=0,42 м. Определить разрежение под поршнем (рис. 4).

Задача 13. Сосуд, имеющий форму конуса с диаметром основания D, переходит в цилиндр диаметром d (рис. 5). В цилиндре перемещается поршень с нагрузкой G=3000 Н. Размеры сосуда: D=1м; d=0,5 м; h=2 м; плотность жидкости r =1000 кг/м³. Определить усилие, развиваемое на основание сосуда.

Задача 14. Вода плотностью r₂=1000 кг/м³ и минеральное масло плотностью r₁=800 кг/м³, находящиеся в закрытом резервуаре, сжимают воздух избыточным давлением р₀ (рис. 6). поверхность раздела минерального масла и воды находятся на расстоянии h₁=0,3 м от свободной поверхности. Показание U образного ртутного манометра h^/=0.4 м. Разница высот свободных поверхностей жидкостей в резервуаре и ртутном манометре h=0,4 м. Определить давление воздуха на свободной поверхности р₀.

Задача 15. Изучить равновесие системы трех жидкостей, находящихся в У- образной трубке, представленной на рис. 7. определить z₀, z₁, z₂, z₃ если z₀–z₁=0,2 м; z₁+z₂=1 м; z₃–z₂=0,1 м; r₀=1000кг/м³; r₂=13600 кг/м³; r₃=700 кг/м³.

Задача 16. Несмешивающиеся жидкости с плотностями r₁, r₂ и r₃ находятся в сосуде (рис. 8). Определить избыточное давление на основание сосуда р_изб, если r₁=1000 кг/м³; r₂=850 кг/м³; r₃=760 кг/м³; h₁=1 м; h₂=3 м; h₃=6 м;

Задача Разность давления между двумя горизонтальными цилиндрическими сосудами (рис. 9), наполненными водой и газом (воздухом), измерена с помощью дифференциального манометра, наполненного спиртом (r₂) и ртутью (r₃). Зная давление воздуха над свободной поверхностью воды в одном из сосудов, определить давление газа p, если p_возд=2,5∙10⁴ Н/м²; r₁=1000 кг/м³; r₂=800 кг/м³; r₃=13600 кг/м³; h₁=0,2 м; h₂=0,25 м; h=0,5 м.

Задача 17.Двойная U-образная трубка заполнена двумя жидкостями таким образом, что свободная поверхность во внутреннем ответвлении трубки находится на одном уровне (рис. 10). Рассчитать плотность r₂, если r₁=1000 кг/м³; h₁=0,8 м; h₂=0,65 м.

Задача 18. Показание манометра, расположенного на расстоянии h₁=м от днища резервуара, р_ман=5 Н/см². Определить высоту свободной поверхности бензина Н в резервуаре (рис. 11), если r_б=850 кг/м³.

Задача 19. Два закрытых сосуда содержат воду. Свободные поверхности расположены по отношению к плоскости сравнения О-О на высотах h₁=1 м и h₂=1,8 м (рис. 12). Показание манометра р₁=1,2∙10⁵ Н/м², разница уровней ртути в дифференциальном манометре Dh=200 мм. Определить давление на свободную поверхность второго резервуара р₂.

Задача 20. Какую силу нужно приложить к поршню 2, чтобы уравновесить действие силы Р₁, действующей на поршень 1 диаметром d (рис. 13), если Р₁=147 Н; D=300 мм; d=50 мм; h=300 мм; r_в=1000 кг/м³?

Задача 21. Каждая сила должна быть приложена к поршням А и В для уравновешивания системы поршней А, В, С (рис. 14), если h=80 см; D=40 см; d=5 см; Р₁=72,64 Н; r_в=1000 кг/м³?

Задача 22. Вследствие опускания поршня весом G в закрытый резервуар под действием силы Р жидкость поднялась в пьезометре на высоту x (рис. 15). Определить величину x, если Р=300 Н; G=200 Н; d=0,1 м; h=0,4 м; r=1000 кг/м³.

Задача 23. На зафиксированный на полу поршень опирается цилиндрический сосуд без днища, заполненный водой. Определить величины давления р₁ и р₂ (рис. 16), если вес сосуда G=10³ Н; r=1000 кг/м³; а=0,8 м; D=0,4 м.

Задача 24. Система трех поршней в сообщающихся сосудах (рис. 17) находится в равновесии под действием трех сил Р₁, Р₂, Р₃ (с учетом веса поршней). Площади поршней соответственно S₁, S₂, S₃. Определить высоты h₁ и h₂, если Р₁=1300 Н; Р₂=1000 Н; Р₃=800 Н; S₁=0,4 м²; S₃=0,6 м²; S₃=0,9 м²; r=1000 кг/м³.

Задача 25. В системе трех поршней (рис. 17) определить изменение сил Р₁ и Р₂. Площади поршней: S₁=0,4 м²; S₃=0,6 м²; S₃=0,9 м²; высоты: h₁=3,3 см и h₂=2,2 см; r=1000 кг/м³.

Задача 26. Определить давление пара в цилиндре поршневого парового насоса (рис. 18) золотниковая коробка, обеспечивающая возратно-поступательное движение поршня в паровом цилиндре, не показана), необходимое для подачи воды на высоту Н = 58 м, если диаметры цилиндров d₁=0,3 м; d₁=0,18 м.

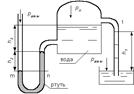Рисунок 1	Рисунок 2
Рисунок 3	Рисунок 4
Рисунок 5	Рисунок 6
Рисунок 7	Рисунок 8
Рисунок 9	Рисунок 10
Рисунок 11	Рисунок 12
Рисунок 13	Рисунок 14
Рисунок 15	Рисунок 16
Рисунок 17	Рисунок 18