Уравнение неразрывности. Уравнение Бернулли

Уравнение неразрывности потока (уравнение баланса расхода) справедливо для установившегося движения, отражает свойства несжимаемости жидкости и сплошности её движения и записывается в следующем виде:

ω₁V₁ = ω₂ V₂ = const, (13)

где ω₁ иω₂ – площади соответствующих живых сечений; V₁ и V₂ – средние скорости в соответствующих сечениях.

Из этого уравнения следует:

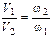, (14)

т.е. средние скорости обратно пропорциональны соответствующим площадям живых сечений.

Уравнение Бернулли для потока реальной жидкости (уравнение баланса энергии) справедливо для установившегося движения, выражает закон сохранения энергиипотока движущейся жидкости и записывается в удельной форме (относительно единицы веса жидкости) для двух сечений и горизонтальной плоскости сравнения в следующем виде:

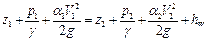, (15)

где 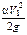, 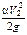– удельная кинетическая энергия соответственно в первом и втором сечениях (скоростной напор);

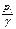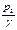, – удельная потенциальная энергия давления соответственно в первом и втором сечениях (пьезометрическая высота);

z₁, z₂ – удельная потенциальная энергия положения соответственно в первом и втором сечениях (геометрическая высота, т.е. расстояние по высоте от плоскости сравнения до центра тяжести сечения);

h_W – потери энергии при движении потока жидкости от первого сечения до второго (потери напора);

α–коэффициент Кориолиса, учитывающий неравномерность распределения скорости по живому сечению;

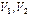– средние скорости в соответствующих живых сечениях;

p₁, p₂ – избыточное давление в центре тяжести соответствующих сечений;

Задачи

Задача 40. Сифон длиной l=l^¢+l^¢¢=25 м и диаметром d=0,4 м (рис. 31) позволяет перетекать воде из одного резервуара в другой. Центральная часть сифона поднимается на высоту h₁ = 2 м над свободной поверхностью жидкости. Разница уровней в резервуарах z=2,5 м. Коэффициент потери напора по длине l=0,02, коэффициент высоты местных потерь: входа z₁=0,5, выхода z₂=1, поворота трубопровода z₃=0,4. Определить расход воды в сифоне.

Задача 41.Через трубопровод диаметром d=100 мм движется с расходом Q=8 л/с (рис. 32). С помощью U – образного ртутного манометра между сечениями 1-1 и 2-2,расположенными на расстоянии l=50 м друг к другу, берется разность показаний h=52 мм. Относительная плотность ртути r =13600 кг/м³. Определить коэффициент потери напора на трениеl.

Задача 42.Центробежный насос должен обеспечить расход Q=0,1м³/с и давление на выходе р₂=4,7∙10⁴ Па. Всасывающая труба имеет диаметр d=0,3 м и длину L=24 м, а также фильтр на входе, имеющий местный коэффициент сопротивления z=5. Всасывание воды осуществляется из открытого резервуара (рис. 33). коэффициент потерь на трение l=0,02, коэффициент местных сопротивлений z_пов=0,2. Определить высоту всасывания Н_вс.

Задача 43. Два резервуара, содержащие воду (резервуар А закрыт, резервуар В открыт и связан с атмосферой), соединены с помощью трубопроводов с диаметрами d₁=70 мм и d₁=100 мм и длинами l₁=3 м l₂=5 м (рис. 34). Разность уровней воды в резервуарах Н=5 м. Предположим, что уровни 1-1 и 5-5 остаются постоянными. Определить расход воды Q, если р_м=20∙10⁴ Па; l=0,02; 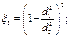z₄=1.

Задача 44. Определить расход воды Q в трубе диаметром d₁ =250 мм, имеющий плавное сужение до диаметра d₂ =125 мм, если показания пьезометром: до сужения h₁ = 50 см; в сужении h₂ = 30 см. Температура воды 20˚С (рис. 35).

Задача 45. Имеется центробежный насос (рис. 36) производительностью Q =9000 л/с, состоящий из всасывающего и нагнетательного трубопроводов. На входе во всасывающий трубопровод диаметром d₁=30 см, давление составляет p₁=200 мм рт. ст., в нагревательном трубопроводе диаметром d₁=20 см, находящемся на высоте z=1,22 м над осью всасывающего трубопровода, давление p₂=7 H/см². Определить гидравлическую мощность насоса.

Задача 46. Определить расход жидкости через зазор между цилиндром и поршнем, если d₁=20,04 см, d₂=20 см, длина сопряжения l=15 см. Поршень неподвижный. Перепад давления Dр=20 МПа, вязкость жидкости μ =170 ∙ 10^-4 Н∙с/м².

Задача 47. Определить повышение давления в трубе диаметром d = 5 см с толщиной стенки d =2 мм при гидравлическом ударе. Скорость потока в трубе v =7 м/с. Модуль упругости жидкости Е_ж=2700 МПа, плотность жидкости r =900 кг/м³. Модуль упруго­сти материала трубы Е_т=2∙10⁵ МПа.

Задача 48.Определить число Рейнольдса и режим движения воды в водопроводной трубе диаметром d=300 мм при расходе Q=0,136 м³/с и температуре воды 10 °С.

Задача 49.По трубопроводу диаметром d=75 мм транспорти­руется нефть плотностью r = 850 кг/м³ с коэффициентом динамиче­ской вязкости m = 0,03 Н∙с/м². Скорость течения V =1 м/с. Опреде­лить гидравлический уклон i.

Задача 50.Определить потери напора по длине при равномер­ном движении жидкости по трубопроводу со средней скоростью V_cp=0,4 м/с, если коэффициент кинематической вязкости жидкости g= 0,4∙10⁴ м²/с, диаметр трубопровода d=100 мм, его длина l =1000 м.

Задача 51. Сложный горизонтальный трубопровод, состоящий из двух параллельных ветвей (рис. 37), транспортирует воду с расхо­дом Q=20 л/с. Рассчитать расходы Q₁ и Q₂ в параллельных ветвях, если l₁=30 м; l₂=50 м; d₁=35 мм; d₂=50 мм; коэффициенты по­терь напора на трение l₁=0,04 и l₂=0,02; коэффициент местных потерь x_кр=1,6.

Задача 52. По трубопроводу, соединяющему два резервуара (рис. 38), в которых поддерживаются постоянные уровни, перетекает вода с плотностью ρ=1000 кг/м³. Диаметр трубопровода d=20 мм. В верхнем баке поддерживается избыточное давление р_изб=15 кПа, а в нижнем- вакуумметрическое давление р_вак=7 кПа. Разность уровней в баках H=5 м. Определить расход жидкости, если коэффициент гидравлического трения λ = 0,028, а длина трубопровода l =15 м. Местными потерями напора пренебречь.

Задача 53. Определить расход воды через сифонный трубопровод (рис. 39), если высота H₁=1 м, Н₂=2 м, Н₃=4 м. Общая длина трубы l =20 м, диаметр d = 20 мм. Режим течения считать турбулентным. Учесть потери на входе в трубу ζ₁ = 1, в коленах ζ₂ = 0,2, в вентиле ζ₃ = 4, на трение в трубе λ = 0,035. Подсчитать вакуум в верхнем сечении х-х трубы, если длина участка от входа в трубу до этого сечения l_х = 8 м.

Задача 54.Определить потребный напор, который необходимо создать в сечении 0-0 для подачи в бак воды (рис. 40) вязкостью ν =0,008 Ст, если длина трубопровода l = 80 м, его диаметр d=50 мм, расход жидкости Q = 15 л/с, высота H₀ =30 м, давление в баке р₂ =0,2 МПа, коэффициент сопротивления крана ζ₁=5, колена ζ₂=0,8, а шероховатость стенок трубы Δ=0,04. Потерями на расширение потока пренебречь.

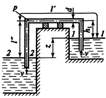Рисунок 31	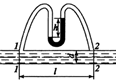Рисунок 32
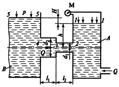Рисунок 33	Рисунок 34
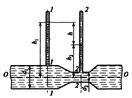Рисунок 35	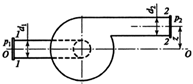Рисунок 36
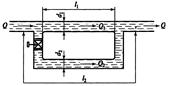Рисунок 37	Рисунок 38
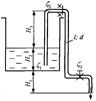Рисунок 39	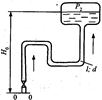Рисунок 40