Сила давления жидкости на поверхности

Сила давления жидкости на плоскую стенку определяется по формуле

, (8)

гдеh_c - глубина погружения центра тяжести плоской стенки, м;

F - площадь стенки, м².

Величинаназывается силой избыточного давления. Точка её приложения не совпадает с центром тяжести фигуры и называется центром давления (рис. 1).

Рисунок 1. Определение центра давления

АВ – след плоской стенки; ox, oy – оси координат;

a - угол наклона стенки к горизонту

Определяется центр давления по формуле:

(9)

гдеy_d – расстояние от свободной поверхности до центра давления (считая по наклону стенки),

;

y_c– расстояние от свободной поверхности до центра тяжести стенки (считая по наклону стенки),

;

– момент инерции фигуры относительно оси, проходящей через центр тяжести фигуры.

Центр давления располагается всегда ниже центра тяжести стенки на величину.

В частном случае для плоской прямоугольной стенки, когда верхняя кромка её совпадает с уровнем свободной поверхности, глубина погружения центра давления равна двум третьим высоты.

Сила давления жидкости на цилиндрическую поверхность определяется как равнодействующая двух сил - горизонтальной и вертикальной

, (10)

где Р_x – горизонтальная составляющая; Р_z – вертикальная составляющая.

Величина Р_x определяется по формуле

, (11)

где F_z – площадь вертикальной проекции цилиндрической стенки, м²;

h_c – глубина погружения центра тяжести этой проекции, м.

Учитывая угол наклона равнодействующей силы Р к горизонту, горизонтальная составляющая равна , а вертикальная составляющая равна .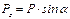

Величина Р_z определяется по формуле:

, (12)

где V_о – объем тела давления АВВ^I, то есть объем, заключенный между цилиндрической поверхностью АВ, пьезометрической плоскостью ОХ (свободная поверхность) и вертикальной проектирующей плоскостью В^IВА, построенной по периметру цилиндрической поверхности (рис. 2).

Рис. 2. Объём тела давления

Задачи

Задача 27. Определить силу суммарного давления воды на плоский щит, перекрывающий канал, и усилие, которое необходимо приложить для подъема щита. Ширина канала b=1,8 м, глубина воды в нем h=2,2 м. Вес щита G=15 кН. Коэффициент трения щита по опорам f=0,25 (рис. 19).

Задача 28. Щит, перекрывающий канал, расположен под углом a=45º к горизонту и закреплен шарнирно к опоре над водой (рис. 20). определить усилие, которое необходимо приложить к тросу для открывания щита b = 2 м, глубина воды перед щитом Н₁=2,5 м, а после щита Н₂ =1,5 м, шарнир расположен над высоким уровнем воды на расстоянии Н₃ =1 м.

Задача 29.Определить силу давления на вертикальную стенку ABCD сосуда, полностью заполненного водой (рис. 21), и положение центра давления, если L = 32 м; l = 26 м; h = 18 м; р = 10³ кг/м³.

Задача 30. Определить силы давления жидкости на стенки и основание открытого сосуда, если l=5м; b = 3м; r = 1000 кг/м³; h = 2 м; a = 60° (рис. 22).

Задача 31. Определить силу давления воды Р' на крышку, пере­крывающую прямоугольное отверстие в плоской стенке резервуара (рис. 23), вертикальную координату h_д точки ее приложения и уси­лие N, которое необходимо приложить к крышке в точке К,если размеры отверстия В=30см, H=20 см, расстояние от верхней кромки отверстия до свободной поверхности воды а=120 мм, рас­стояние между точкой Ки осью шарнира О-О l= 250 мм, показа­ние манометра, установленного на верхней крышке резервуара, р_м=0,2∙10⁵ Па.

Задача 32. Определить силы давления на боковые поверхности резервуара, заполненного бензином (рис. 24), и координаты центров давления, если a = 60°; b=1м; h = 4 м; r = 750 кг/м³.

Задача 33. Определить силу F, необходимую для удержания вер­тикальной стенки шириной b = 4 м и высотой Н=5,5 м (рис. 25) при глубине воды слева h₁ = 5 м, справа h₂ = 2м; r =1000 кг/м³.

Задача Определить результирующую силу давления на пло­скую поверхность Аи положение точки ее приложения (рис. 26). Показание манометра на закрытом резервуаре, заполненном водой, р_м= 5000 Н/м²; H=4 м; D = 1 м; r = 10³ кг/м³.

Задача 34.Определить силу суммарного давления на торцовую плоскую стенку цилиндрической цистерны диаметром d=2,4 м и точку ее приложения. Высота горловины h_r=0,6 м. Цистерна заполнена бензином до верха горловины (рис. 27).

Задача 35. Определить силу давления воды на цилиндрическую стенку резервуара (рис. 28), а также угол наклона к горизонту линии действия этой силы а, если радиус стенки R= 2 м, ширина стенки В= 3 м, высота уровня воды в трубке пьезометра, установленного на верхней крышке резервуара, h = 0,5 м.

Задача 36. В стенке резервуара просверлен трап, который за­крывается полусферической крышкой радиусом R = 0,1 м и весом 200 Н (рис. 29). Какова должна быть высота Hводы в резервуаре, чтобы крышка открылась?

Задача 37. На плоской боковой поверхности резервуара име­ется полусферическая крышка-трап (рис. 30). Высота жидкости над центром трапа Н = 3,5 м, показание вакуумметра, установленного на резервуаре p_вак= 0,5 ∙ 10⁵ Н/м². Определить результирующее давление на крышку трапа, если D = 0,6 м; r = 10³ кг/м³.

Задача 38.Круглое отверстие в вертикальной стенке закрытого резервуара с бензином перекрыто сферической крышкой (рис. 31). Радиус сферы R=0,3 м, глубина жидкости над центром тяжести отверстия Н=2,0 м. Определить величину и направление результирующей силы давления жидкости на крышку при показании манометра р=150 кПа.

Задача 39.В верхней стенке призматического сосуда с водой (рис. 32) имеется полусферическая крышка R= 0,7 м. Определить отрывающее усилие, воспринимаемое болтами крышки, если показания манометра р_м =200 кПа, глубина h=1,5 м.

Рисунок 19	Рисунок 20
Рисунок 21	Рисунок 22
Рисунок 23	Рисунок 24
Рисунок 25	Рисунок 26
Рисунок 27	Рисунок 28
Рисунок 29	Рисунок 30
Рисунок 31	Рисунок 32