
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сопротивления и области их применения
Для определения потерь по длине применяется формула Дарси-Вейсбаха
h1 = λ  .
.
Чтобы выбрать соответствующую зависимость для λ, предлагается простой алгоритм. Обычно заданы: расход Q, диаметр трубы d, кинематический коэффициент вязкости ν и величина эквивалентной шероховатости kэ (из таблиц) для данного материала. В табл. 10.1 приведены значения kэ для труб из разных материалов.
Таблица 10.1
| Трубы, их материалы и состояние стенок | k, мм |
| Стальные цельнотянутые новые | 0,02 – 0,07 |
| Стальные цельнотянутые, находившиеся в эксплуатации | 0,2 – 0,5 |
| Стальные цельнотянутые после продолжительной эксплуатации, сильно заржавленные | До 1,0 |
| Железные оцинкованные | 0,15 – 0,18 |
| Чугунные асфальтированные новые | 0,13 |
| Чугунные новые | 0,25 |
| Чугунные, находившиеся в эксплуатации | 1,4 |
Определяют:
а) среднюю скорость V=  =
=  ;
;
б) число Рейнольдса Rе =  ;
;
в) относительную шероховатость  .
.
1. Если Rе < 2300, то имеет место ламинарный режим и
λ =  . (10.1)
. (10.1)
2. Если Rе > 4000, то определяют величину параметра
Rе  .
.
3. Если Rе  < 10, то имеет место гладкостенная зона сопротивления и λ определяется по формуле Блазиуса
< 10, то имеет место гладкостенная зона сопротивления и λ определяется по формуле Блазиуса
λ =  . (10.2)
. (10.2)
4. Если 10 < Rе  < 500, то имеет место доквадратичная зона сопротивления и λ определяется по формуле Альтшуля
< 500, то имеет место доквадратичная зона сопротивления и λ определяется по формуле Альтшуля
λ = 0,11  (10.3)
(10.3)
5. Если Rе  > 500, то имеет место квадратичная зона сопротивления и λ определяется по формуле Шифринсона
> 500, то имеет место квадратичная зона сопротивления и λ определяется по формуле Шифринсона
λ = 0,11 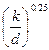 . (10.4)
. (10.4)
Задача 10.1. Определить, какой степени средней скорости пропорциональны потери по длине в каждой из зон сопротивления.
Решение. Используется формула Дарси-Вейсбаха (9.14) и зависимость для 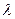 в соответствующей зоне сопротивления.
в соответствующей зоне сопротивления.
1. Для ламинарного режима  64/ Rе и потери hl выразятся так
64/ Rе и потери hl выразятся так
 или, сокращая числитель и знаменатель на V,
или, сокращая числитель и знаменатель на V, 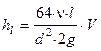 .
.
В правой части последней формулы первый сомножитель не зависит от скорости и величина hl имеет вид hl =  , т.е. потери в ламинарной зоне сопротивления пропорциональны первой степени скорости.
, т.е. потери в ламинарной зоне сопротивления пропорциональны первой степени скорости.
2. В зоне квадратичного сопротивления λ определяется по формуле λ=0,11  , а потери выразятся так hl=0,11
, а потери выразятся так hl=0,11  .
.
Так как первый сомножитель в правой части не зависит от скорости, то потери hl пропорциональны скорости в квадрате, откуда и название зоны – квадратичная зона сопротивления.
Задача 10.2. Поток в трубе находится в квадратичной зоне сопротивления. Как изменятся потери по длине в этой трубе, если расход в ней увеличить в два раза?
Решение. Учитывая решение задачи 10.1, заключаем, что если расход увеличить в два раза, то и средняя скорость увеличится в два раза и поэтому (поскольку зона квадратичная) потери возрастут в 22, т.е. в 4 раза.
Задача 10.3. Отрезок трубы внутренним диаметром d1=100 мм был заменен отрезком трубы такой же длины, но внутренним диаметром d2, в 2 раза меньшим: d2=50 мм.
Определить, как изменились потери на этом участке при такой замене. Расход воды остался таким же; считаем для упрощения решения, что в обоих случаях квадратичный режим, изменение λ не учитываем.
Решение. Для решения задачи достаточно определить отношение потерь h1 в трубе с d1=100 мм к h2 в трубе с d2=50 мм. Выражения для h1 и h2 по формуле Дарси-Вейсбаха (9.14)
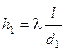
 и
и 
 . Их отношение
. Их отношение  . (10.5)
. (10.5)
Согласно уравнению неразрывности
 или
или 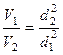 .
.
Если возведем обе части последнего равенства в квадрат, получим
 . (10.6)
. (10.6)
Подставляя (10.6) в (10.5), имеем окончательно  .
.
Если 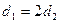 , то
, то
 .
.
Таким образом, потери увеличились в 32 раза! Если учесть, что 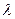 также зависит от диаметра, то получим несколько меньшее число.
также зависит от диаметра, то получим несколько меньшее число.
Этот же результат возможно получить, оценивая порядок величин, а именно, потери выражаются зависимостью
 или
или  . (10.7)
. (10.7)
Средняя скорость выражается так
V=Q/S или V~1/d 2,
т.е. при  обратно пропорциональна квадрату диаметра, а средняя скорость в квадрате, соответственно, обратно пропорциональна четвертой степени диаметра, т.е.
обратно пропорциональна квадрату диаметра, а средняя скорость в квадрате, соответственно, обратно пропорциональна четвертой степени диаметра, т.е.
V2 ~1/d 4 . (10.8)
Имея в виду (10.7) и (10.8), получаем в данном случае
h1~1/d 5,
т.е. потери обратно пропорциональны диаметру в пятой степени. Этот результат имеет большое значение при гидравлических расчетах водопроводных сетей.
Дата добавления: 2015-04-18; просмотров: 347; Мы поможем в написании вашей работы!; Нарушение авторских прав |