
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
При турбулентном режиме
С помощью полуэмпирической теории турбулентности получена зависимость для распределения скорости в круглой трубе при турбулентном режиме
u = A lny + C,(9.10)
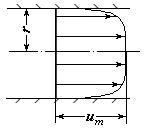
где A и C – некоторые постоянные; y – расстояние от стенки. Таким образом, скорости в турбулентных потоках распределены по логарифмическому закону; такое распределение скорости характеризуется быстрым нарастанием ее у стенки и почти постоянной величиной в центральной части (рис. 9.5).
 Для распределения скорости в трубах часто используют эмпирические формулы, наиболее простой из которых является степенная
Для распределения скорости в трубах часто используют эмпирические формулы, наиболее простой из которых является степенная
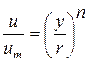 , (9.11)
, (9.11)
где um – значение скорости на расстоянии  от стенки (на оси трубы); r – радиус трубы; u – скорость на
от стенки (на оси трубы); r – радиус трубы; u – скорость на
Рис. 9.5 расстоянии y от стенки трубы.
Показатель степени n в этой формуле не постоянен и убывает с возрастанием числа Re. Так, при Re = 4·103 он равен 1/6, а при Re = 32·105 – 1/10. Среднее значение n, соответствующее гладкостенному режиму, равно 1/7. Для этого случая зависимость (9.11) называется «закон одной седьмой» для распределения скорости
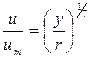 . (9.12)
. (9.12)
Отношение vср и umax в условиях ламинарного режима равно 0,5, а при турбулентном режиме, как показывают опыты,– 0,85 – 0,95.
Для инженерных расчётов возможно получить um и значение осредненной скорости в круглой трубе на любом расстоянии от стенки. Предварительно необходимо убедиться, что режим движения турбулентный. Вначале расход жидкости в трубе делят на площадь её сечения и определяют Vср
Vср=  .
.
Затем находят um
um= 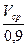 .
.
Для определения u подставляют все уже известные величины в (9.12) и получают
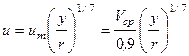 .
.
Дата добавления: 2015-04-18; просмотров: 312; Мы поможем в написании вашей работы!; Нарушение авторских прав |