
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение Бернулли для потока реальной жидкости. В инженерной практике при решении гидравлических задач всегда имеются в виду потоки (трубы, каналы) конечных размеров
В инженерной практике при решении гидравлических задач всегда имеются в виду потоки (трубы, каналы) конечных размеров, по которым движется реальная (обладающая вязкостью) жидкость. Движение потока реальной жидкости или газа всегда сопровождается потерями энергии. Это происходит даже при движении потока по совершенно гладким трубам. Причиной таких потерь является трение о стенки трубопроводов и внутреннее трение в жидкости (по причине вязкости). Если представить течение идеальной жидкости в горизонтальной трубе одинакового диаметра, то в любых двух сечениях потока, как следует из (8.8), давление будет постоянное. Если жидкость вязкая, то, как следует из опытов, давление вдоль трубы уменьшается (рис. 8.6); это происходит из-за преобразования механической энергии в теплоту за счет трения.


Рис. 8.6 Рис. 8.7


 При течении в трубопроводе вязкой жидкости возникает «прилипание» ее к стенкам и вследствие вязкости образуются эпюры скоростей, как на рис. 8.7. Уравнение закона сохранения энергии для единицы веса вязкой жидкости можно составить следующим образом. Допустим, что поток вязкой жидкости в сечении 1 обладает удельной энергией
При течении в трубопроводе вязкой жидкости возникает «прилипание» ее к стенкам и вследствие вязкости образуются эпюры скоростей, как на рис. 8.7. Уравнение закона сохранения энергии для единицы веса вязкой жидкости можно составить следующим образом. Допустим, что поток вязкой жидкости в сечении 1 обладает удельной энергией
|
 +
+ 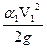 , (8.10)
, (8.10)
(в этом выражении и далее, где имеется в виду поток вязкой жидкости, значения давления  и геометрической высоты z приняты в центре тяжести живого сечения).
и геометрической высоты z приняты в центре тяжести живого сечения).
Аналогично, поток в сечении 2, находящемся за сечением 1, обладает удельной энергией
е2=z2+  +
+  . (8.11)
. (8.11)
Разность удельных энергий в этих двух случаях


будет представлять собой удельную энергию потока, перешедшую в тепло вследствие трения. Величину  также называют «потерей» энергии или «потерей» напора, что не совсем точно; энергия теряться не может - она лишь преобразуется из одного вида в другой.
также называют «потерей» энергии или «потерей» напора, что не совсем точно; энергия теряться не может - она лишь преобразуется из одного вида в другой.
Окончательно уравнение сохранения энергии – уравнение Бернулли – для потока вязкой жидкости будет иметь вид
z1+  +
+ 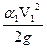 =z2+
=z2+  +
+  + hw , (8.12)
+ hw , (8.12)
где z1, z2 – высоты положения произвольных точек, выбранных в двух сечениях потока (чаще всего выбирают точки центров тяжести сечений);
р1, р2 – давления в сечениях 1 и 2 в тех же точках; V1, V2 – средние скорости в сечениях 1 и 2; 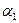 и
и  - коэффициенты кинетической энергии;
- коэффициенты кинетической энергии;
 – потери удельной энергии (напора) на участке между рассматриваемыми сечениями.
– потери удельной энергии (напора) на участке между рассматриваемыми сечениями.
Необходимо обратить внимание, что в выражениях (8.10), (8.11) и (8.12) имеется в виду средняя скорость потока, равная V =  , где Q - расход, S - площадь поперечного сечения. Обычно в расчетах она может быть легко найдена или задается, и величина удельной кинетической энергии, вычисленная по средней скорости, должна быть скорректирована по величине действительной кинетической энергии. С этой целью вводится корректирующий коэффициент, который называется также коэффициентом Кориолиса (или коэффициентом кинетической энергии), косвенно он учитывает неравномерность распределения скорости по сечению; обычно при равномерном турбулентном движении в трубах
, где Q - расход, S - площадь поперечного сечения. Обычно в расчетах она может быть легко найдена или задается, и величина удельной кинетической энергии, вычисленная по средней скорости, должна быть скорректирована по величине действительной кинетической энергии. С этой целью вводится корректирующий коэффициент, который называется также коэффициентом Кориолиса (или коэффициентом кинетической энергии), косвенно он учитывает неравномерность распределения скорости по сечению; обычно при равномерном турбулентном движении в трубах 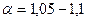 .
.
Геометрический смысл каждого члена в уравнении для удельной энергии был рассмотрен в 8.1. Выражения (8.10) и (8.11) могут быть представлены как суммы трех вертикальных отрезков z,  и
и  , и каждая сумма является геометрическим образом полной удельной энергии в данном сечении. Для того, чтобы представить изменение полной удельной энергии вдоль потока, достаточно в нескольких сечениях построить вертикальные отрезки, соответствующие полным удельным энергиям в данных сечениях, и соединить концы линий.
, и каждая сумма является геометрическим образом полной удельной энергии в данном сечении. Для того, чтобы представить изменение полной удельной энергии вдоль потока, достаточно в нескольких сечениях построить вертикальные отрезки, соответствующие полным удельным энергиям в данных сечениях, и соединить концы линий.
При движении вязкой жидкости линия удельной энергии не горизонтальная, а наклонная, так как удельная энергия потока при движении вязкой жидкости уменьшается в направлении движения.
Величина
i2 =  ,
,
где в числителе – разность полных энергий в двух сечениях; l – расстояние между этими сечениями, называется гидравлическим уклоном. Его можно представить так: i2 =  или i2 =
или i2 =  .
.
Каждое слагаемое в (8.10) и в (8.11) представляет, как это было выведено в (8.1), определенный вид механической энергии. При движении жидкости потенциальная энергия может переходить в кинетическую и наоборот, а суммарная механическая энергия убывает по причине перехода некоторой ее части в тепло.
Уравнение Бернулли является одним из основных уравнений в гидравлике, поэтому техника и методика его использования важны. Перечислим основные условия его применения.
1. Выбираются два сечения потока, в которых геометрические и кинематические параметры изменяются плавно, движение поэтому называется плавно изменяющимся и давления в сечениях изменяются по гидростатическому закону.
2. Назначается положение плоскости сравнения – плоскости отсчета геометрических высот z.
3. При написании уравнения Бернулли для сечений, где движение плавно изменяющееся, выбираются точки, для которых записываются высоты z и давления p в любом месте выбранных сечений – на дне, на свободной поверхности, в центре тяжести живого сечения, на оси трубы и т.д. Лучше всего выбирать эти точки или на свободной поверхности (в этом случае чаще всего p1=p2=pат) или в центре тяжести живых сечений.
4. Имея в виду общий вид уравнения Бернулли для потока реальной жидкости (8.12), записывают все его члены применительно к выбранной плоскости отсчета и двум сечениям. В случае успешного применения (совместно с уравнением неразрывности) должно остаться одно неизвестное.
Задача 8.3. Применить уравнение Бернулли к потоку реальной жидкости в трубе постоянного диаметра.
Решение. В данном случае в любом сечении движение является плавно изменяющимся и поэтому два сечения выбираются произвольно. Высоты z1 и z2 отсчитываются от оси трубы и давления в сечениях принимаем равными p1 и p2. Расход жидкости в сечениях 1 и 2 одинаковый и в силу постоянства диаметра скорости в сечениях также равны: V1 и V2.Общий вид уравнения Бернулли такой

 z1 +
z1 + 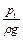 +
+  =z2+
=z2+  +
+ 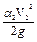 +hw .
+hw .
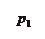
 Применительно к данному случаю имеем z1=z2=0 (т.к. ось трубы совпадает с осью сравнения и проходит через центры выбранных сечений), V1=V2,
Применительно к данному случаю имеем z1=z2=0 (т.к. ось трубы совпадает с осью сравнения и проходит через центры выбранных сечений), V1=V2, 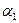 =
=  и уравнение Бернулли принимает вид
и уравнение Бернулли принимает вид
 .
.
Из последнего равенства следует, что разность уровней в пьезометрах точно равна потерям удельной механической энергии, т.е. той части механической энергии потока, которая необратимо преобразовалась в тепло. Потери всегда положительны, hw>0 , поэтому высота жидкости в левом пьезометре больше, чем в правом. Таким образом, расход вдоль потока остается постоянным, скорость не меняется, а убывание механической энергии сказывается в убывании давления вдоль потока.
Дата добавления: 2015-04-18; просмотров: 331; Мы поможем в написании вашей работы!; Нарушение авторских прав |