
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Потери по длине и местные
Для решения различных задач первостепенное значение имеет уравнение Бернулли, поскольку оно связывает скорость и давление в сечении; в него входит величина, выражающая потери механической энергии. Поэтому для решения практически любой задачи необходимо знать, какими зависимостями выражается величина потерь. Представим себе бак, из которого жидкость может выливаться по трубе в атмосферу (рис. 9.6); скорость течения жидкости и расход могут изменяться с помощью крана К. Если кран К закрыт, то жидкость в трубе Т неподвижна, силы трения отсутствуют, уровни в пьезометрах равны (как в сообщающихся сосудах) и жидкость обладает запасом потенциальной энергии; никаких превращений энергии при этом не происходит.
Если кран К открыть, то под действием силы тяжести вода будет вытекать в атмосферу, начнется движение жидкости. При этом, как при всяком движении, возникнут силы трения (так как жидкость вязкая) о стенки трубы и внутри самой жидкости. На жидкость силы трения действуют в сторону, противоположную направлению скорости. Как всегда при действии сил трения механическая энергия преобразуется в тепло и количество механической энергии уменьшается вдоль потока.


а б
Рис. 9.6
Применим уравнение Бернулли в общем виде
z1 +  +
+ 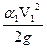 = z2 +
= z2 +  +
+  + hw
+ hw
к сечениям потока 1 и 2, в которых расположены пьезометры (рис. 9.6, б), выбрав ось сравнения 0-0 совпадающей с осью горизонтальной трубы T. Как следует из рис. 9.6, б, z1 = z2 = 0 и несмотря на то, что механическая энергия жидкости вдоль потока уменьшается, средняя скорость не изменяется, так как расход остается постоянным. Поэтому V1 = V2 и α1 = α2. С учетом последних замечаний уравнение Бернулли принимает вид
 =
=  + hw
+ hw
или
hw =  -
-  = h1 – h2 = Δh. (9.13)
= h1 – h2 = Δh. (9.13)
Таким образом, потери удельной механической энергии можно измерить обычной линейкой; еще можно заметить в данном случае, что несмотря на частичное превращение механической энергии, кинетическая энергия остается постоянной вдоль потока, а потенциальная энергия убывает. Энергию (или напор), на величину которой удельная механическая энергия убывает, называют «потерянной» энергией («потерями» энергии или «потерями» напора). На самом деле никаких потерь энергии не происходит, а имеет место преобразование механической энергии в тепловую в результате трения. Если представить течение в длинной трубе, то по всей ее длине условия перехода механической энергии в тепловую будут одинаковые – т.е. будет одинаковое трение по всей длине. В этом случае потери будут называться потерями по длине и их величина пропорциональна длине трубы.
Формула для потерь энергии по длине имеет вид
 (9.14)
(9.14)
и называется формулой Дарси-Вейсбаха.
В этой формуле приняты следующие обозначения: hl – потери напора на длине l; V – средняя скорость; d – диаметр трубы; g – ускорение свободного падения; λ – коэффициент, учитывающий состояние стенок трубы и режим движения.
При расчетах потерь напора по формуле Дарси-Вейсбаха длина трубы, ее диаметр, расход задаются и определение hl встречает затруднение только в связи с вычислением коэффициента λ.
Дата добавления: 2015-04-18; просмотров: 349; Мы поможем в написании вашей работы!; Нарушение авторских прав |