
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифференциальные уравнения равновесия жидкости. Представим в жидком теле (рис.6) прямоугольный параллелепипед abсd с бесконечно малыми ребрами dx, dy
Представим в жидком теле (рис.6) прямоугольный параллелепипед abсd с бесконечно малыми ребрами dx, dy, dz, параллельными осям координат X, Y, Z/
Напишем условия равновесия этого параллелепипеда, рассматриваяя, прежде всего проекции на ось Xвсех действующих на него сил.
1. Поверхностные силы. Пусть на пересечении диагоналей параллелепипеда в точке s давление равно P. Проведем через s линию, параллельную оси х. Эта линия пересечет грани ab и cd в точках m и n.

Рис.6
.
Давление в точке m будет равно  , а в точке n -
, а в точке n - 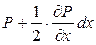 . Сила давления на грань ab будет равна
. Сила давления на грань ab будет равна 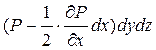 , а на грань cd соответственно
, а на грань cd соответственно  .
.
2. Массовые силы. Равнодействующая массовых сил дает на ось проекцию  , где ρ - плотность жидкости, а X - проекция на ось xсилы, действующей на единицу массы рассматриваемой жидкости.
, где ρ - плотность жидкости, а X - проекция на ось xсилы, действующей на единицу массы рассматриваемой жидкости. 
При отсутствии других сил для равновесия нужно выполнить условие

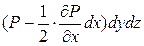 -
-  +
+ 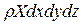 =
=  (7)
(7)
Разделив последнее выражение на  , получим
, получим

Аналогично, для проекций на оси y и zполучим:


Последние уравнения можно преобразовать следующим образом:

 (8)
(8)

Это и есть дифференциальные уравнения равновесия жидкости, выведенные Л. П. Эйлером в 1755 г.
Из (11) после преобразований можно получить:
 (9)
(9)
Левая часть уравнения (9) представляет собой полный дифференциал, следовательно,
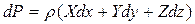 (10)
(10)
Для поверхности равного давления, т. е. для такой поверхности, все точки которой имеют постоянное давление (dP=0). Тогда и правая часть уравнения (10) тоже должна равняться нулю. Таким образом, поверхность равного давления определяется уравнением:
 (11)
(11)
Левая часть уравнения (10) представляет полный дифференциал, следовательно, и правая часть должна быть также полным дифференциалом. При постоянной плотности это условие будет выполнено, если в правой части уравнения (10) множитель в скобках будет полным дифференциалом; для этого необходимо и достаточно, чтобы существовала такая функция
U (х, у, z), частные производные которой по x, yиz соответственно были равны X, Y, Z, т. е.
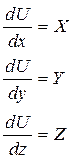 (12)
(12)
Воспользовавшись уравнениями (10), вместо (8) можно написать

Проинтегрировав, получим
 , (13)
, (13)
где С - постоянная интегрирования. Для определения ее должны быть известны в какой-либо точке жидкости давление Р0 и функция Uo. Для этой точки по формуле (13) имеем

откуда  .
.
Подставив это значение С в уравнение (13), получим
 (14)
(14)
Пользуясь выражением (14), можно найти величину давления в разных точках жидкости. В частном случае, когда на жидкость из массовых сил действует только сила тяжести,
X = 0; Y =0; Z = -g.
Следовательно,
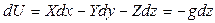 .
.
Тогда (U-U0)= -g (z - z0) и уравнение (12) принимает вид

Учитывая, что (z0 - z)=h , получим
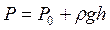
Дата добавления: 2015-04-18; просмотров: 267; Мы поможем в написании вашей работы!; Нарушение авторских прав |