Сила давления жидкости на плоскую фигуру

Пусть жидкость действует на наклоненную под углом α к горизонту стенку АВ (рис. 10). Определим величину силы давления p на фигуру mn, расположенную на этой стенке Для удобства рассмотрения стенку АВ повернем вокруг оси Y до совмещения с плоскостью чертежа. Тогда на плоскости чер­тежа XOY увидим фигуру mn в натуральную вели­чину (фигура mn на чер­теже заштрихована).

Рис.10

Обоз­начим площадь фигуры mn буквой ω. Для вычисле­ния величины силы Р опре­делим сначала силу давле­ния dР на элементарную площадку dω, находящую­ся на глубине h и имеющую координату у. Тогда

Но на основании формулы (16) р = ρgh, а поэтому dР = ρghdω, а так как h= у sinα (рис. 10), то

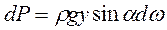(20)

Для определения силы давления на всю фигуру mn проинтегрируем выражение dР по площади ω:

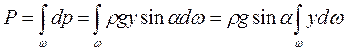(21)

при этом ρ, g и sinα как постоянные величины вынесены за знак интеграла; представляет собой статический момент площади относительно оси X. Как известно, этот момент равен площади фигуры ω, умноженной на коорди­нату у_с центра тяжести С относительно той же оси:

Подставляя это значение в (24), получим

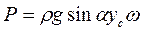(22)

Согласно рисунку 11

где h_c - глубина погружения центра тяжести С, а поэтому

(23)

На основании же формулы (16) величина ρgh_c представ­ляет собой манометрическое давление р_с в центре тяжести фигуры тп, поэтому окончательно имеем

(24)

т. е. сила давления на плоскую фигуру равна давлению в центре тяжести этой фигуры, умноженному на площадь фигуры.