Потери напора при внезапном расширении трубы

Рассмотрим установившееся движение жидкости на участке горизонтальной трубы (рис. 36), поперечное се­чение которой резко увеличивается.

Как показывают опыты, поток при выходе из трубы с

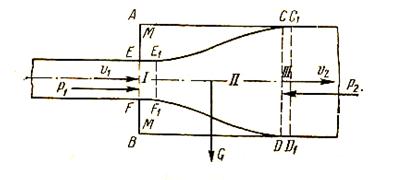
Рис. 36

меньшим диаметром быстро расширяется и в сечении; CD заполняет всю трубу. Между основным потоком и стенками трубы образуется кольцевое пространство ММ, заполненное жидкостью, не участвующей в общем поступательном движении, по­чему область М нередко называют «мертвым простран­ством».

При движении жидкости от сечения EF к сечению CD часть энергии жидкости теряется на преодоление сопро­тивлений. Для определения величины этих потерь выделим из жидкости объем АСDВА и применим к нему теорему о ко­личестве движения, согласно которой при установившемся движении приращение количества движения тела за единицу времени равно сумме проекций (на направле­ние движения) всех действующих на тело сил.

Определим приращение количества движения за еди­ницу времени. За единицу времени через сечение EF, а также и через сечение CD протекает объем жидкости, равный расходу Q, а частицы жидкости, находившиеся в сечениях EF и CD, переместятся соответственно в се­чения Е₁F₁ и С₁D₁ Следовательно, жидкость, занимая в первоначальный момент объем ACDBA, через единицу времени будет занимать объем А С₁D₁В F₁F Е₁EА.

Для краткости объем жидкости EE₁F₁FE обозначим римской цифрой I, остальную часть объема ACDBA - цифрой II и объем C С₁D₁DC - цифрой III. Тогда коли­чество движения в начальный момент равно

к.д.I + к.д.II, (73)

а количество движения через единицу времени

к.д.II + к.д.III, (74)

Следовательно, для определения приращения коли­чества движения за единицу времени необходимо из вы­ражения (74) вычесть выражение (73). Тогда прираще­ние количества движения за единицу времени составит

к.д.III - к.д.I (75)

Количество движения III равно mv₂, где v₂ - ско­рость в сечении CD. Количество движения I равно mv₁,где v₁ - скорость в сечении EF.

Следовательно, приращение количества движения за единицу времени будет (mv₂ - mv₁)

Масса mжидкости, протекающей в единицу времени, равна ρQ, или ρωv₂, где ω - площадь поперечного се­чения трубы большего диаметра. Отсюда получаем, что приращение количества движения за единицу времени равно

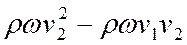(76)

Теперь найдем сумму проекций сил на направление движения. На объем ACDBA действуют следующие силы, для которых будем указывать и соответствующие про­екции:

1. Сила Р₁ на грань АВ. Эта сила равна р₁ω, где р₁ - давление в центре тяжести сечения АВ. Проекция этой силы на направление движения равна (+ р₁ω).

2. Сила Р₂ на грань CD. Эта сила равна р₂ω, где р₂ -
давление в центре тяжести сечения CD. Проекция этой
силы на направление движения равна (-р₂ω).

3. Реакции боковых стенок на жидкость. Эти силы нормальны к оси трубы, следовательно, их проекция на направление движения равна нулю.

4. Сила тяжести жидкости G в объеме ACDBA. Сила G вертикальна, а поэтому ее проекция на направление движения равна нулю.

5. Силы трения жидкости о поверхность трубы на участке между сечениями АВ и CD.Эти силы, как показывает опыт, малы по сравнению с силами Р₁ и Р₂, а потому ими можно пренебречь.

Таким образом, сумма проекций сил, действующих на объем AСОВА, равна

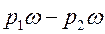(77)

На основании теоремы о количестве движения выра­жение (77) должно равняться выражению (74), т. е.

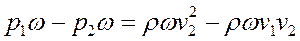(78)

Сократив на ω и разделив на ρg левую и правую части выражения (78), получим

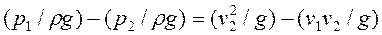(79)

Теперь напишем уравнение Бернулли для сечений АВ и CD:

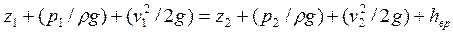(80)

где 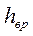- потери напора при внезапном расширении. Поскольку z₁ = z₂, выражение (80) можно перепи­сать в следующем виде:

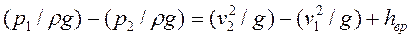(81)

В выражениях (79) и (81) левые части равны, следо­вательно, в них равны и правые части, т. е

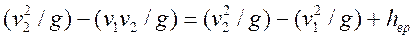
Из этого выражения получаем

(82)

Последнее выражение носит название формулы Борда. В частном случае, когда скорость v₂мала по сравне­нию со скоростью v₁,

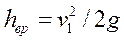
т. е. местные потери напора в этом случае равны удель­ной кинетической энергии.