
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Распределение скоростей по живому сечению
Возьмем круглую трубу радиусом r (рис. 31). Определим скорость и в произвольно взятой точке М, отстоящей от оси трубы на расстоянии у. Проведем через точку М радиусом, равным y концентрическую поверхность. Основное уравнение равномерного движения (51) для жидкости, движущейся внутри проведенной концентрической поверхности, дает
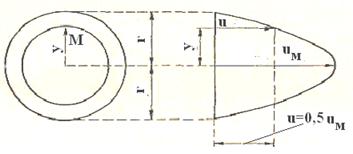
Рис.31
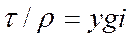 (53)
(53)
(так как гидравлический радиус R = у/2)
Сила трения на единицу площади

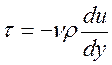 (54)
(54)
где знак минус взят из-за того, что скорость, как показывает опыт, убывает от оси трубы к стенкам, и, следовательно, градиент 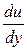 отрицателен. Подставив значение τ в формулу (53), получим
отрицателен. Подставив значение τ в формулу (53), получим
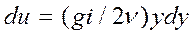
После интегрирования
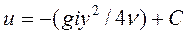 (55)
(55)
Постоянную С определим из условия, что при у= r скорость и= 0, так как частицы жидкости, смачивая стенку, прилипают к ней, т. е. имеют нулевую скорость.
Подставив в формулу (53) эти значения, будем иметь
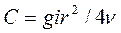
Подставив это значение С в уравнение (55), получим
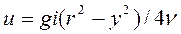 (56)
(56)
Из формулы (54) следует, что скорости при ламинарном режиме распределяются по параболическому закону.
Максимальная скорость, очевидно, получится при значении у = 0, т. е. на оси

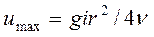
Дата добавления: 2015-04-18; просмотров: 264; Мы поможем в написании вашей работы!; Нарушение авторских прав |