Уравнение Даниила Бернулли для частицы жидкости

Пусть частица жидкости (рис. 25) движется от точки 1 в сечении А-Адо точки 2 в сечении В-В. Подсчитаем удельную энергию, которой обладает частица в точках 1 и 2. Обозначим u₁, p₁ скорость частицы и давление в точке 1 с координатой z_l а u₂, р₂ — скорость частицы и давление в точке 2 с координатой z₂. При этих обозначениях для частицы в сечении А-А:

z₁ - удельная энергия положения; ( 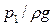)- удельная энергия давления; ( 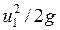) - удельная кинетическая энергия.

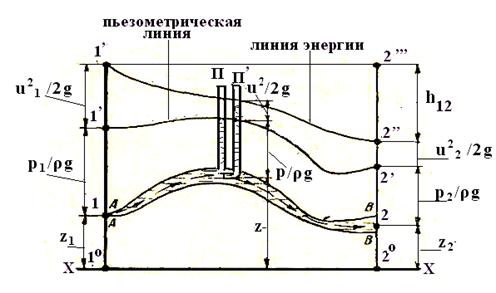
Рис.25.

Для частицы в сечении В-В:

z₂ - удельная энергия положения; - удельная энергия давления; 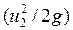-удельная кинетическая энергия.

Полная удельная энергия частицы в сечении А-А,очевидно, равна

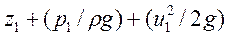(37)

а в сечении В-В

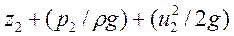(38)

Для частицы идеальной жидкости полная удельная энергия остаётся постоянной величиной. Для частицы реальной жидкости трехчлен (37) больше трехчлена (38), так как на пути 1-2 часть энергии израсходуется на преодоление различных сопротивлений. Эта часть удельной энергии называется потерей напора и обозначается буквой h_1-2. Тогда на основании закона о сохранении энергии можно написать

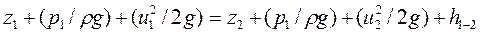(39)

Уравнение (39) называется уравнением Да­ниила Бернулли для частицы жид­кости. Все члены этого уравнения имеют размерность длины, и поэтому его можно изобразить графически (рис 25). Откладывая в каждой точке отрезка 1^o-2^o оси А последовательно координаты частицы жидкости z, высо­ты p/ρg и скоростные высоты u²/2g, получим линии 1-2, 1'-2'и 1''-2''. Линия 1-2 - это траектория движения частицы жидкости, линия 1'-2', называемая пьезо­метрической линией, показывает изменение удельной потенциальной энергии z + p/ρg, а линия 1''-2'' - изменение полной удельной энергии частицы и носит название линии энергии. Все эти линии в общем
случае будут кривыми, причем линия энергии может только
опускаться так как энергия в направлении движения
уменьшается.

Проведя горизонтальную прямую 1''-2''', получим для сечения В-В отрезок 2"-2'",который равен потере напора h_1-2 на пути 1-2, а вертикальные отрезки между прямой 1"-2'"и линией энергии 1''-2'' представляют со­бой потери напора на участке от сечения А-Адо рас­сматриваемого сечения.

В заключение отметим, что величины z + p/ρg и u²/2g можно измерить, поставив пьезометр П и изогнутую труб­ку П'(рис.26). В пьезометре Пжидкость поднимается до пьезомет­рической линии, а в трубке П' - до линии энергии. Разность уровней в П и П' даст величину u²/2g.