Уравнение Даниила Бернулли для потока

Уравнение Даниила Бернулли легко распространить и на поток жидкости (рис. 26) при условии, что в живых сечениях, для которых применено это уравнение, движение плавноизменяющееся.

Рассмотрим напорный поток 1-2(рис. 26). Пусть жидкость движется от живого сечения 1 до живого сече­ния 2, а площади этих живых сечений равны ω₁ и ω₂. Подсчитаем полную удельную энергию потока для сечения 1.

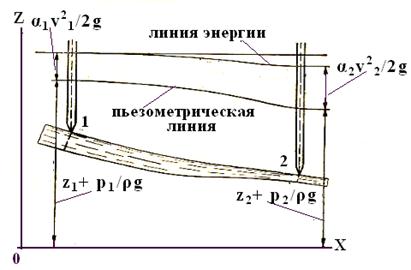
Рис.26

Удельная потенциальная энергия жидкости во всех точках сечения 1-2 величина постоянная и равна верти­кальному расстоянию от плоскости сравнения X (рис. 26) до свободной поверхности (до уровня) жидкости в пьезо­метре. Удельную потенциальную энергию жидкости для сечения 1обозначим z₁+ p₁/ρg .

Удельная кинетическая энергия жидкости, протекаю­щей через живое сечение, может быть выражена через среднюю скорость при условии введения некоторого коэф­фициента. Этот коэффициент в гидравлике обозначается α и называется коэффициентом Кориолиса. Следовательно, удельная кинетическая энергия для сечения равна

Таким образом, полная удельная энергия для сече­ния 1 составляет

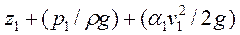(40)

Совершенно аналогично для сечения 2 полная удельная энергия равна

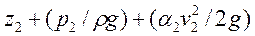(41)

Для потока идеальной жидкости полная удельная энергия потока остаётся неизменной. Для реальной жидкости трехчлен (40) больше трехчлена (41), так как на пути от сечения 1 до сечения 2часть энергии израсходуется на преодоление различных сопротивлений. Обозначая поте­рянную удельную энергию (потерю напора) буквой h_1-2 можем написать

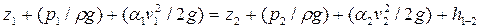(42)

Уравнение (42) называется уравнением Да­ниила Бернулли для потока. Коэффициент Кориолиса α, представляющий собой отношение действительной кинетической энергии к кинетической энергии, вы­численной при условии движения всех частиц в сечении с одной и той же скоростью. Опыты показывают, что α обычно изменяется в пределах от 1,03 до 1,1.

Поскольку коэффициент α близок к единице, то очень часто полагают α = 1, и тогда уравнение Бернулли для потока принимает вид

(41)

Следует отметить, что удельная потенциальная энергия равна расстоянию от плоскости сравнения X до уровня жидкости в пьезометре только в том случае, когда давление в сечении изменяется по гидростатическому закону. Если же давление в сечении изменяется не по гидростатическому закону, то удельная потенциальная энергия не равна расстоянию от плоскости сравнения до уровня жидкости в пьезометре. Так, например, если давле­ние по всему живому сечению равно барометрическому (для всех точек живого сечения манометрическое давле­ние р = 0), то в этом случае удельная потенциальная энергия равна удельной энергии положения, т. е. расстоя­нию от плоскости сравнения до центра тяжести потока. Для потока (рис. 27), так же как и для частицы, линия, показывающая изменение удельной потенциальной энер­гии называется пьезометрической линией, а ли­ния, показывающая изменение полной удельной энер­гии, - линией энергии.