ВЫТЕКАНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ

1. Вытекание жидкости через отверстие втонкой стенке

Рассмотрим случай вытекания жидкости в атмосферу через отверстие площадью ω (рис.45).

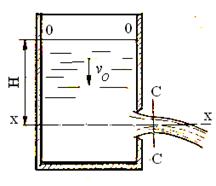
Рис.45.

Струя при вытекании через отверстие постепенно сжи­мается. Ближайшее к отверстию наименьшее живое сечение С-С, в котором движе­ние можно рассматривать плавноизменяющимся, называется сжатым сечением. Обо­значим площадь сжатого сече­ния С-С буквой ω_сж. Отноше­ние

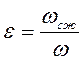(91)

называется коэффициентом сжа­тия.

Так как отдельные струйки в сжатом сечении почти параллельны, то можно считать, что давление в нем равно давлению окружающей среды, т. е. в данном случае барометрическому давлению р_б.

Обозначим Н высоту уровня жидкости над центром тяжести отверстия, v -скорость в сжатом сечении. Выберем за ось координат горизонтальную ось X-X, проходящую через центр тяжести отверстия, и напишем уравнение Бернулли для сечения О-О и сжатого сече­ния С-С:

,

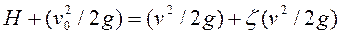где v₀ – скорость воды в сосуде.

Пренебрегая величиной (v₀²/2g) (ввиду ее малости по сравнению с Н), получим

,

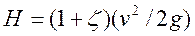откуда скорость вытекания

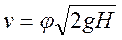(92)

где 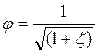называют коэффициентом скорости. Коэффициент скорости является отношением скоростей реальной и идеальной жидкости при вытекании через отверстия и насадки.

Для вычисления расхода жидкости через отверстие надо скорость умножить на площадь сжатого сечения:

Учитывая, что

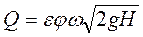(93)

Обозначим

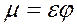(94)

Величина μ называется коэффициентом расхода (отношение расхода реальной жидкости через отверстие к расходу идеальной жидкости при вытекании через отверстия и насадки). Выражение (94) является безразмерной формой для уравнения неразрывности потока, а (93) принимает вид

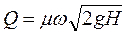(95)