Истечение из незатопленного отверстия.

Рассмотрим истече­ние жидкости из малого незатопленного отверстия в тонкой стенке резервуара. Малым отверстием называют отверстие, вертикальный размер которого (высота, диаметр) не больше 0,1 Н (Н — напор над центром тяжести отверстия). Незатопленным называют отвер­стие, из которого жидкость истекает в атмосферу или другую газо­вую среду.

Говоря о тонкой стенке, имеем в виду, что отверстие в ней имеет острые края, и линейный размер отверстия l (например, диаметр) и толщина стенки δ связаны зависимостью δ < 3l.

При истечении из малого отверстия с острыми краями струя жидкости на некотором расстоянии от стенки сжимается (рис. 35). Это явление объясняется инерцией частиц жидкости, движущейся при подходе к отверстию по криволинейным траекториям, которые лишь на некотором расстоянии за отверстием движутся параллель­но друг другу.

Как показывает опыт, для круглого отверстия наиболее сжатое сечение струи находится за стенкой на расстоянии, равном примерно 0,5 диаметра отверстия. ношение площади этого сечения S_СЖ к площади отверстия S₀ называют коэффициентом сжатия струи при ис­течении: ε = S_сж/S₀ [118]

Для определения истечения жид­кости из малого отверстия в верти­кальной стенке в атмосферу при по­стоянном напоре воспользуемся урав­нением Бернулли. Проведем плоскость сравнения 0—0 через центр тяжести сечения струи. Так как

Рис.37

площадь сечения 1-1 значительно превышает площадь сечения II-II то скоростью жидкости в сечении I-I можно

пренебречь. Тогда уравнение Бернулли при­мет вид

[119]

где Н₀ – геометрический напор; р_о - давление на свободную поверхность; р₂ и υ₂ — давление и средняя скорость жидкости в сечении II – II; h_f — гидравлические потери напора, которые для малого отверстия в тонкой стенке определяются только мест­ным сопротивлением: h_f = h_m = ξ Тогда уравнение [119]примет вид [120]

Если давление в сечении II – II мало отличается от атмосферного и давления в сечении I - I, можно принять p₂ = p_o Тогда уравнение [120] запишем в виде

[121]

Откуда -

коэффициент скорости, представляющий собой отношение действительной скорости истечения реальной жидкости к скорости истечения идеальной жидкости, для которой ξ = 0 и φ= 1. Поэтому скорость истечения идеальной жидкости опре­деляют по формуле Торричелли: [122]

Соответствующий ей расход идеальной жидкости, вытекающей из отверстия с площадью живого сечения S₀, Q_т =

Действительный расход реальной жидкости, вытекающей из такого же отверстия,

[123]

где μ_s коэффициент расхода отверстия, который представляет собой отношение действительного расхода к теоретическому при истечении жидкости из отверстия:

Если отверстие в стенке или дне сосуда расположено так, что остальные стенки оказывают влияние на истечение жидкости из отверстия, то происходящее в этом случае сжатие струи называют полным несовершенным. Такое сжатие струи наблюдается, когда отверстие в стенке расположено относительно какой-нибудь другой стенки или дна ближе, чем указано ранее (отверстие 2). При полном несовершенном сжатии коэффициент сжатия несколько больше, чем при полном совершенном, поэтому и коэффициент

расхода больше.

В практике встречаются случаи, когда отверстие, из которого происходит истечение непосредственно примыкает к другой стенке или дну сосуда (отверстие 3). У такой стенки сжатия струи не про­исходит и оно называется неполным.

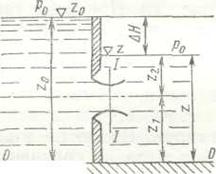
Истечение жидкости из затопленного отверстия.Затоплен­ным называют отверстие, из которого истекает жидкость, расположенное ниже уровня жидкости (рис. 36). Примером такого вида истечения является работа шлюзов, очистных сооружений промыш­ленных стоков, нефтеловушек и т. п. Для определения скорости истечения струи из затопленного отверстия составим уравнение Бернулли для двух сечений: начального, совмещенного со сво­бодной поверхностью питающего водоема, и конечного I - I, совпадающего со сжатым сечением струи. Скорость жидкости на свободной поверхности пренебрежимо мала по сравнению со ско­ростью истечения из затопленного отверстия. Давление в сече­нии I - I распределяется по законам гидростатики. Уравнение Бернулли для этого случая имеет вид [124]

где p₁ — давление в центре тяжести отверстия истечения: р₁ = р_о +ρgZ₂

С учетом равенства Z₁ + Z₂ = Z и обозначения Z_o-Z =ΔH

получим формулу для определения скорости истечения: аналогичную формуле Торричелли [122], но здесь ΔH — разность уровней в водоемах.

При определении скорости истечения реальной жидкости полу­чаем формулу, аналогичную формуле (83), но с учетом сделанной оговорки.

Расход жидкости из затопленного отверстия можно определить по формуле [123], в которую вместо Н₀ следует подставить разность уровней в водоемах.