Режимы движения реальных жидкостей.

Существуют два ре­жима движения жидкостей: ламинарный и турбулентный. При ламинарном режиме отдельные струйки или слои жидкости дви­жутся параллельно, не смешиваясь, при турбулентном — ча­стицы жидкости движутся беспорядочно по разнообразным не­определенным траекториям, а само движение сопровождается поперечным перемещением жидкости и характеризуется пульса­цией скорости и давления.

Исследования О. Рейнольдса показали, что режим движения жидкости в общем случае зависит от скорости движения, размеров потока, плотности и вязкости жидкости. Комплекс указанных ве­личин, характеризующих режим движения жидкости, называют числом Рейнольдса:

Re = [90]

где R — гидравлический радиус потока; μ — динамическая вяз­кость.

Число Рейнольдса — величина безразмерная.

Так как согласно формуле μ/ρ = v, то формулу [87] можно записать в виде

Re = [88] где v – кинематическая вязкость жидкости

Формулу (40) применяют при определении числа Рейнольдса для потока любого сечения. Для круглых цилиндрических труб с внутренним диаметром d

Re_d = 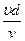[91]

Поскольку для таких труб гидравлический радиус R = 4d, то Re = 4Re_d.

Границы существования режимов движения жидкости опреде­ляются двумя критическими значениями числа Рейнольдса: нижним Re_{Kp. нижн} и верхним Re_{Кр верхн}. При Re < Re_Kp наблюдается устой­чивый ламинарный режим течения жидкости, при Re > Re_{Кр верхн.} — устойчивый турбулентный режим. В интервале чисел Рейнольдса Re_{Кр. верхн} > Re > Re_{Kp нижн.} режим течения жидкости неустойчивый; ла­минарный режим легко переходит в турбулентный.

В настоящее время принимают нижнее критическое число Рейнольдса равным

Re_{Кр. нижн} = 250 ... 500; для цилиндрических труб Re_dк_Р = 1000...2000. При проведении гидравлических расчетов очень часто принимают Re_{Кр. верхн} = 575 и Re_{d Кр} — 2300.

На практике чаще наблюдается турбулентный режим течения жидкости, например, при движении воды в трубах из-за ее срав­нительно малой вязкости и большой скорости течения. При дви­жении вязких жидкостей (нефти, масла и др.), а также при дви­жении жидкостей с малой вязкостью, но с небольшой скоростью, наблюдается ламинарный режим течения.

Ламинарному и турбулентному режимам движения жидкости соответствует и различное распределение скоростей по живому сечению потока. При ламинарном, режиме течения жидкости по трубе максимальную скорость имеют частицы жид­кости, движущиеся по оси трубы. У стенок трубы скорость стре­мится к нулю, так как частицы как бы прилипают к внутренней поверхности, образуя тонкий неподвижный слой. Исследования показывают, что при ламинарном режиме движения жидкости изменение скорости в поперечном сечении потока происходит по параболическому закону.

При турбулентном режиме течения жидкости распределение скоростей более равномерное по сечению потока, чем при ламинарном режиме Это, происходит вследствие перемешивания при турбулент­ном режиме частиц, движущихся с различными скоростями. При турбулентном режиме слои, прилегающие к стенкам трубы, дви­жутся с малой скоростью, и режим движения здесь ламинарный. Поэтому, строго говоря, чисто турбулентного режима движения жидкости не существует. Однако толщина ламинарного слоя мала в сравнении с толщиной основного потока жидкости, и такой ре­жим течения жидкости принято считать турбулентным.

Практическое применение уравнения Бернулли.

Уравнение Бернулли — основное уравнение гидродинамики — применяют для решения многих теоретических и практических задач: при гидравлическом расчете трубопроводов, насосных установок, гидравлических турбин и т. д. Уравнение Бернулли лежит также в основе принципа расчета различных измерительных приборов, в частности приборов для измерения скоростного напора и рас­хода жидкости.

Измерение скоростного напора. Наиболее простым и распро­страненным прибором для измерения скорости движения жидко­сти является трубка Пито 7, изогнутая под прямым углом и от­крытая с обоих концов (рис. 27). Трубку Пито устанавливают в по­токе открытым суженным концом против движения жидкости, частицы которой у входного отверстия теряют свою кинетическую энергию и производят дополнительное давление на неподвижную жидкость в трубке. В результате этого уровень жидкости в трубке

Пито становится на некоторую высоту Н_с больше уровня в пьезо­метрической трубке 2. Следовательно, трубка Пито позволяет определить полное гидродинамическое давление в данной точке потока жидкости. Скоростной напор

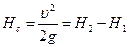[92]

Из этого уравнения можно найти скорость в точке потока жидкости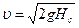

Определение расхода жидкости.

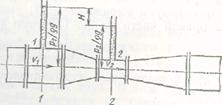
Расход жидкости в трубопро­водах определяют расходомерами. Рассмотрим принцип действия, расходомера Вентури. Прибор состоит из двух конических пат­рубков, соединенных цилиндрическим патрубком, диаметр кото­рого меньше диаметра трубопровода (рис. 32). При прохождении жидкости через сужающийся конический патрубок часть ее по­тенциальной энергии преобразуется в кинетическую. При движе­нии жидкости через расширяющийся патрубок происходит об­ратное явление. Разность показаний установленных в сечениях 1-1 И 2—2 пьезометров позволяет определить среднюю скорость жидкости, а следовательно, и ее расход.

На основании уравнения Бернулли, запишем следующее равенство для сечений

1-1 и 2-2 [93]

Обозначим левую часть уравнения (52) через Н, получим [94]

Пользуясь уравнением неразрывности потока, запишем где S₁и S₂ — соответственно площади сечений 1-1 и 2—2,

Подставляя выражение для υ₂ в уравнение [94] получим

откуда или

где D и d диаметры сечений 1-1 и 2-2

теоретический расход [95]

Для практических расчетов формулу [95] упрощают, заменяя все постоянные величины коэффициентом , называемым постоян­ной расходомера, имеющей для данного прибора вполне опреде­ленное значение: β = mS [96]

где m = Тогда формула [95] примет вид [97]